저번 포스팅까지는 X 변수가 하나라는 가정하에 진행해 왔습니다. 이제 부터는 X가 둘 이상인 multi을 다룹니다.

위 그림처럼, X들이 여러개 나뉘어 졌다. X1: 공부시간, X2: 등하교 시간으로 예를 들수 있겠습니다. 그래서 각각의 변수 데이터를 가지고 해당되는 target 값인 y를 예측하게 됩니다.

X2가 추가가 되었음을 볼 수 있다. 각 theta, X에 대해서 벡터 형식으로 정리가 가능하다. X 벡터의 1인 dummy 변수를 넣어 줘야 dot product 했을때 계산이 가능합니다.

Loss function에 th가 3개로 확장 되었으므로 더이상 평면이 아닌 공간 상에서 표현이 될 것입니다.

전에 배웠던 내용과 다른 점이 있다면 th2가 추가 되었다는 점 뿐이다.

각 th별로 미분을 하면 빨간색과 같은 수식이 나온다. 다만 달라진 점은 X인데 해당 X에 따라서 데이터 어떤 영향을 끼치는지 계속 자각해야 한다.

gradient을 구한뒤 GDM의 수식을 위 처럼 정리 할수 있겠다. th2은 X2에 영향을 받고, th1은 X1에 영향을 받는다는 점이 핵심이다.

Cost도 같은 과정을 거치게 되면 최종적으로 위 그림처럼 정리할 수 있다.

이번엔 X가 m개일 경우를 살펴본다. 예를 들어 100*100 이미지가 있다면 10000개의 X가 존재하고 이를 벡터형식으로 바꾼 모습이 위와 같을 것이다.

각각의 th,X의 벡터을 dot product을 시키면 맨 아래 수식처럼 간단한 형식으로 표현이 가능하다. Loss도 마찬가지로 같은 원리를 통해 간단하게 표한가능하다.

weight M개, bias 1개를 포함한 M+1개를 각각 gradients 구하면 위처럼 정리 할수 있다. m+1 차원의 Gradients가 만들어 진다. weight에는 P라는 첨자가 붙고 bias에는 붙지 않는다는 것에 대한 의미를 까먹지 않도록 상기 시켜야 한다.

Affine function 부분에서 forward, backward propagation이 발생하 넘겨주고, 받는 역할을 하게 된다. 누구에게 넘겨주느냐? Activation Funtion에게 넘겨주게 된다. 이런 전체적인 과정이 딥러닝이 일어나는 과정이다.
왼쪽 그림을 보면 둘로 나눠져 있다. 즉,affine funtion 뒤에 Activation이 붙든, Cross entropy가 붙든, soft max가 붙든, Loss 구하든지, cost를 구하든지 일절 상관이 없다. Affine은 단지 Z값을 전달하고, 자기가 내줬던 값에 대한 편미분 값을 받아서 업데이트 하는 것 뿐이다.
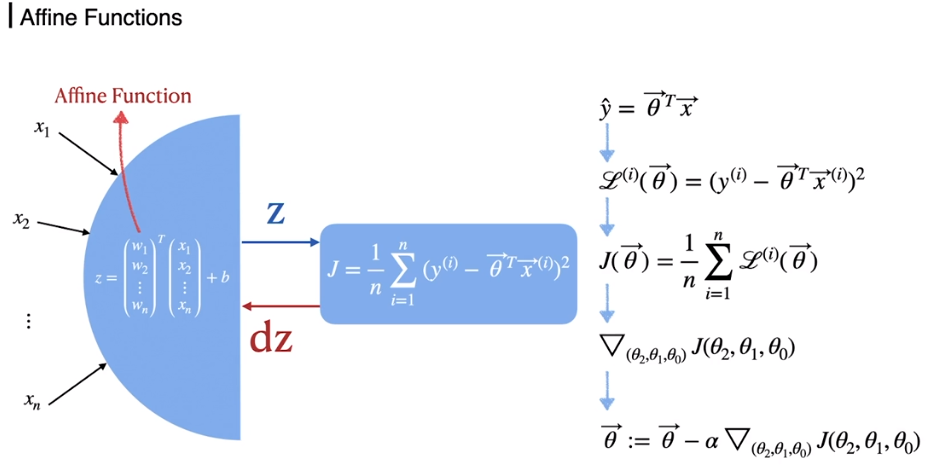
지금까지 배웠던 것을 그림으로 표현하면 위와 같다. Z값을 받고 Loss 혹은 Cost를 구한뒤 편미분을 통해 업데이트가 일어난다. 뉴런 1개에 이와 같은 연산이 발생한다.
multi linear에서는 Loss function이 어떻게 변하는지 알아보자.
Loss funtion
-편의상 두개의 x값을 가지고 진행한다.

각각의 datset에 따른 prediction과 Loss는 위 처럼 구할수 있을 것이다. 이것을 다음에 적용해 보도록 한다.

해당 식과 data가 있을때, 변화를 면밀하게 살펴보기 위해서 세개의 값중 하나를 고정시켜 보도록 한다. 가장 왼쪽은 bias가 학습이 다 됐다는 가정 하에 th의 변화를, 두번째는 th1이 학습완료가 됐다는 가정하에 th2와 th0간에 변화를 나타내고 마지막도 같은 원리로 진행한다.

가장 왼쪽 사진에서 적용된 data는 (1,1)이다. 파란색 식을 보면 (1,1)일때 비율이 같기 때문에(학습량이 같다) a=-x방향의 Loss funtion을 볼수 있다.
두번째 사진에서 적용된 data는 x1의 1뿐이다. 그러면 th2와 th0 간의 비율도 역시 같기 때문에 대각선 방향이며 세번째 그림도 같은 원리로 대각선 방향이다.

첫번째 사진에서 적용된 data는 (2,1)이다. th2가 더 높은 비율을 가지므로 th1보다 빨리 학습 될것이다. 그림에서 보듯이 기울기가 y축 방향으로 붙는걸 확인할수있다. th2방향으로 먼저 projection이 된다.
두번째 그림에서 적용된 값은 x2의 2이다. 파란색 식을 보면 2*a*x2 VS 2*a 이므로 2배차이가 발생한다. 그래서 첫번째 그림처럼 y축에 붙게 된다.
세번째 그림은 th1과 th0은 서로 같은 비율이기 때문에 y = -x 방향의 대각선을 갖게된다.

파란색과 빨간색은 서로 같은 비율이기 때문에 겹쳐있다.

왼쪽그림에서 x2=3, x1=2 일때, 이 둘의 비율 차이가 1.5배이다. 1보다는 크고 2보다는 작은 모습으로 만들어진 것이다.
가운데 그림에서는 비율이 3배 차이가 나기 때문에 기울기가 더욱 기울어진 모습을 보인다.
오른쪽 그림은 비율의 차이가 2배이므로 1보다는 크고 3보다는 작은 모습으로 만들어진다.


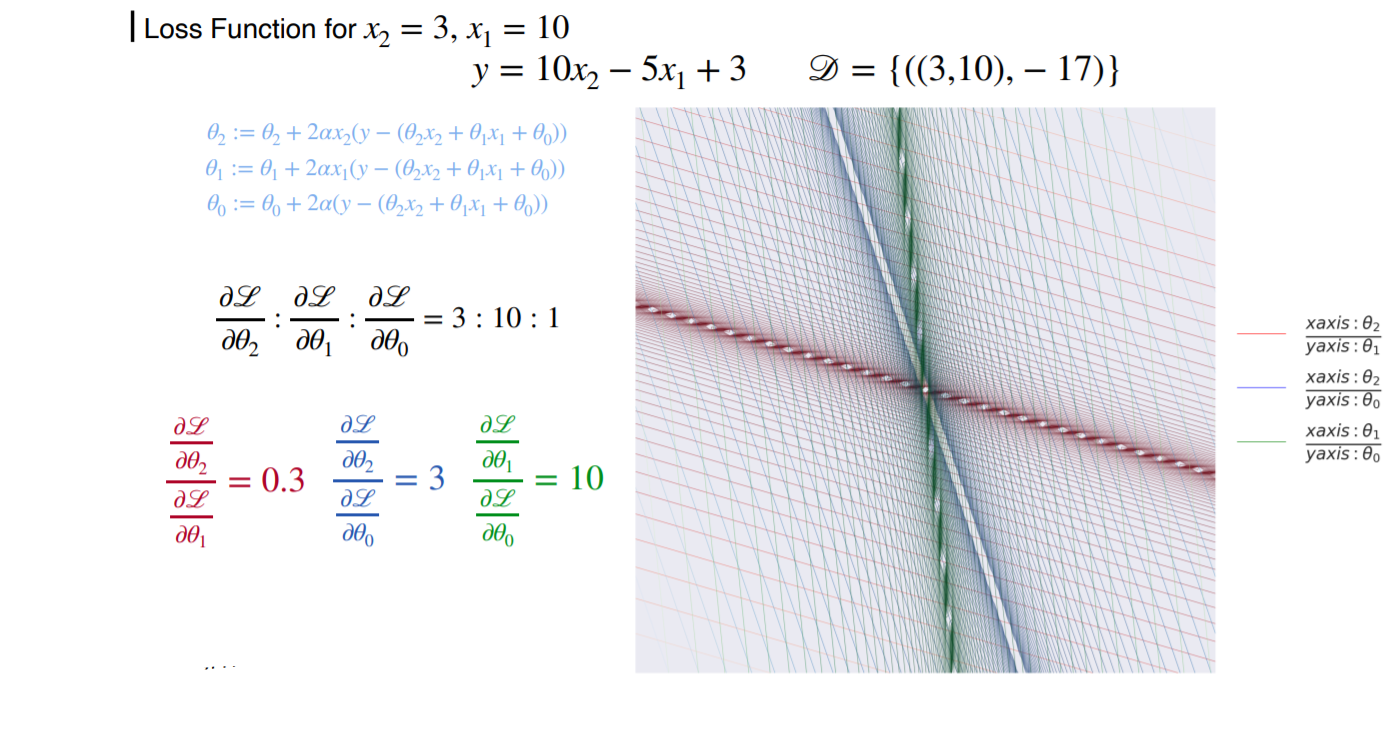
왼쪽그림에서 x1=10, x2= 3 일때, x1이 더 크기 때문에 먼저 학습이 될 것이다. 전에 배웠던 X의 값이 1보다 작을때의 Loss function 형태와 같아진다.
두번째 그림에서는 x2와 bias의 비율 차이가 3배이기 때문에 이와 같이 만들어진다.
세번째 그림에서는 10배 만큼 비율의 차이가 있으므로 y축에 바짝 붙는 형태가 만들어진다.

표준정규분포를 따르는 데이터를 입력으로 넣었을 때는 th들이 균등하게 학습이 되는 특징을 가지고 있다. 위 모습이 가장 "이상적인 학습의 모습"이다.

x2=5로 늘리 다. 또한 Loss의 양을 보면 초반에 초반에만 급격하게 치솟아 올랐다. 이는 급격한 th2의 학습이 원인이다. x값이 크면 Loss의 양도 비례하게 된다. Loss가 크다는 건 학습해야 할 양이 많다는 건데 X값이 너무 커지면 lr로 더욱 작게 설정하여 발산하지 못하도록 해야한다.

x2가 1보다 작은 수 라면, th2만 혼자서 학습속도가 느려진 걸 확인 할수 있다. 하단의 그림을 보면 th1, th0이 먼저 학습할려고 위쪽으로 끌어 당기는 모습이 보인다. 그리고 th1,th0은 같은 학습속도 이므로 좌하단처럼 대각선 모양을 가진다.

극단적으로 0.1를 std로 설정하면 거의 0 근처 값들만 나오게 될 것이다. 그래서 하단 그림을 보면 거~의 학습이 되지 않는다. interation을 많이 주게 되면 결국은 목표값에 도달하겠지만 그만큼 시간과 자원이 소모되는 걸 감안 했을때는 비효율적이다. 또한 중간에 끊기게 되면 th1,th0은 학습이 된 상태될 것이고, th2은 학습이 미완성인 상태로 끝나게 되는 문제점도 있다.
이번엔 평균이 바뀔때 변하는 모습을 보도록 한다.


X2의 평균값 자체가 커지면서 th2의 지배적인 학습이 진행됨을 볼수있다. 가운데를 보면 th2가 자기쪽으로 당기기 때문에 th0에 대한 학습이 지그재그로 천천히 학습이 되는 문제점이 생긴다.

상하단 그림을 비교해 보자. mean값이 커질수록 먼저 학습이 되기 때문에 하단처럼 th2,1이 먼저 치고 올라 가는걸 볼수 있다. 반면 th0은 더욱 느려진다. 왜냐면 Loss가 th2,1에게 많이 뺐겼기 때문이다. 하단의 loss를 보면 평행을 이룰만큼 거의 존재하지 않는다.
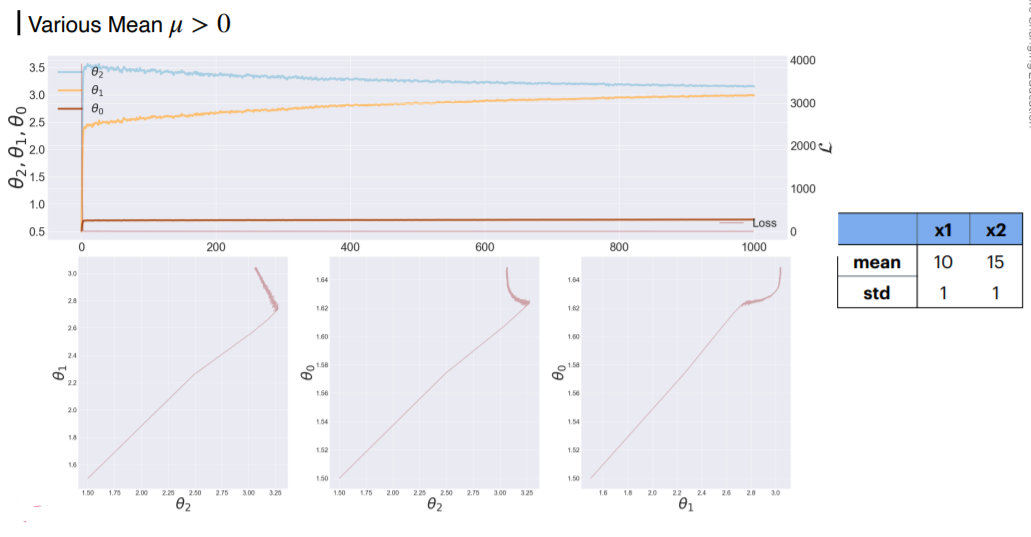
하단을 보면 공통적으로 보이는 것은 th2,1 쪽으로 먼저 빠르게 학습이 된 후에야 th0가 지그재그로 학습 되고 있다.


x2 평균이 -5 음수이다. 이때 특이한 모양이 보이는데 바로 윗 그림을 보면 th0값이 뒤로 오히러 퇴보? 뒤로 당겨지는 모습을 보인다. 이유는 간단하다. -5의 Loss function 방향으로 projection이 되다 보니까 이런 현상이 발생한 것이다. 초기값이 만일 다른 곳에서 출발했다면 또 다른 모습을 보일 것이다.
'Data Diary' 카테고리의 다른 글
| 2021-09-18(따릉이 프로젝트 완성하기 7) (0) | 2021.09.21 |
|---|---|
| 2021-09-15(따릉이 프로젝트 완성하기 6) (0) | 2021.09.15 |
| 2021-09-13(따릉이 프로젝트 완성하기 5) (0) | 2021.09.13 |
| 2021-09-10(딥러닝 수학14_dataset 변화에 따른 th1,th0 학습 시각화) (0) | 2021.09.10 |
| 2021-09-09(따릉이 프로젝트 완성하기 4) (0) | 2021.09.09 |


