*본 내용은 시계열데이터 강의 내용 중 일부분을 요약한 내용입니다
회귀모델을 적용 후 R-squared,F-분포, t검정 등의 결과가 일관성이 없을때 믿어야 할건 데이터 라는 것이다.
일관성이 없다고 효과없는 데이터를 무작정 삭제 하는게 아니라, 시각화를 통해서 종속변수에 영향을 주는 데이터인지 아닌지를 판단해야한다.
모델적용
fit_reg1 = sm.OLS(Y_train, X_train).fit()
display(fit_reg1.summmary())
pred_tr_reg1 = fit_reg1.predict(X_train).values
pred_te_reg1 = fit_reg1.predict(X_test).values
'''
*R-squared
평균치 ybar 보다 적합이 좋은지 나쁜지를 나타낸다
1.00은 모드예측값이 실제값과 모두 동일함을 의미한다
*F-statistic(F검정)
유의확률이 0.00으로 유의수준보다 작으므로, 이 모델링은 효과가 있다.
모든 계수가 효과가 있다
*t 검정
count_diff, count_lag1를 제외하곤 모두 영향력이 없다
F검정에는 모든 계수가 효과 있다고 했는데? 이상함을 감지 해야한다
*잔차 보기
정규분포의 Kurtosis(첨도)는 3이다.
현 Kurtosis는 13078.751, 일반 첨도보다 훨씬 꼬리가 두터운 형태
*정규분포의 Skew(왜도)는 0이다.
현 Skew는 -114.255, negative 형태 (오른쪽 쏠림), 상당히 벗어난 값
*회귀분석 지표가 많은 이유는 모든 결과가 일관성 있을때 까지 시도하라는 의미
*지속적인 튜닝이 필요
*회귀분석은 값만 출력하고, 쓸지 말지는 사람이 선택한다. 따라서 합리적인 근거를 토대로
사용여부를 결정한다. 근거의 대표적인 도구가 시각화이다.
믿어야 할건 알고리즘이 아니라 데이터이다.
'''


- 위 결과에 대한 해석은 실습의 주석처리로 되어있습니다
- 일관성 없는 데이터에 대해서 시각화를 통해 정확한 정보를 얻어낸다
- 이상적인 그림은 모델 적용하기 전 시각화를 통해 변수에 대한 정보를 파악하는게 맞다
시각화
# histogram plot
raw_fe.hist(bins=20, grid=True, figsize=(16,12)) #x를 몇개 그룹으로 나눌것이가: bins
plt.show()
'''
count와 비슷한 분포가 상관관계가 높고, 유의하다고 나올 가능성이 높다
y분포와 비슷하게 만드는 것이 예측에 도움이 될것
'''
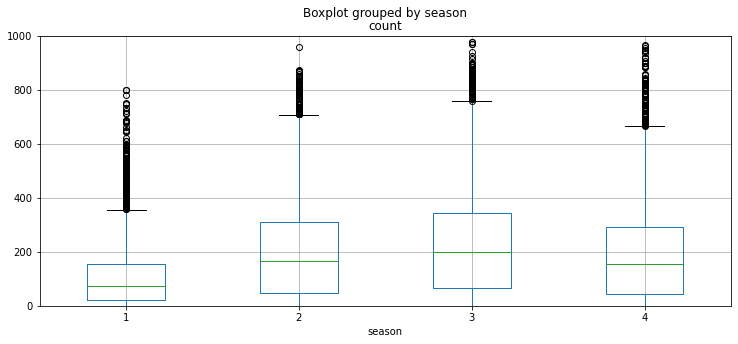
# box plot_계절별 각 수요 관계 파악
raw_fe.boxplot(column='count', by='season', grid=True, figsize=(12,5))
plt.ylim(0,1000)
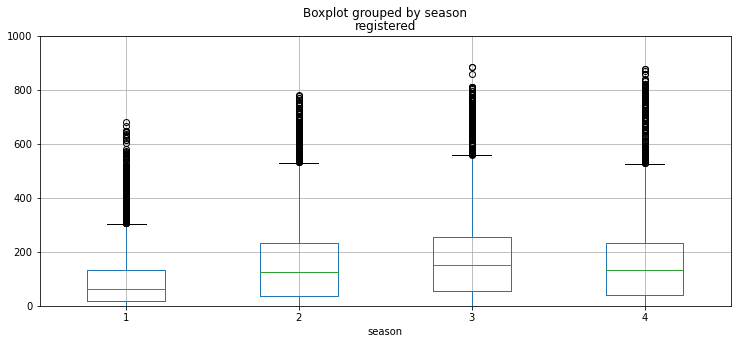
raw_fe.boxplot(column='registered', by='season', grid=True, figsize=(12,5))
plt.ylim(0,1000)
raw_fe.boxplot(column='casual', by='season', grid=True, figsize=(12,5))
plt.ylim(0,1000)
'''
만일 계절의 y분포 네개가 똑같다면 어떨까?
계절에 의한 count 변화는 없다는 의미이며 계절변수가 쓸모 없다는 것
계절별로 패턴이 많이 달라야 예측에 도움이 된다.
'''

# box plot_휴일,평일과 수요(count) 관계 파악
raw_fe.boxplot(column='count', by='holiday', grid=True, figsize=(12,5))
plt.ylim(0,1000)
raw_fe.boxplot(column='count', by='workingday', grid=True, figsize=(12,5))
plt.ylim(0,1000)
'''
휴일과 평일 비교하는 그래프에서, 평일에 수요가 훨씬 많음을 알수있다
분포가 다르고 해석되는 것에 차이가 있으므로 y분포에 도움이 될수 있다.
'''

raw_fe[raw_fe.holiday==0].boxplot(columns = 'count', by ='Hour', grid=True, figsize=(12,5))
plt.show()
raw_fe[raw_fe.holiday ==1].boxplot(columns='count', by ='Hour', grid=True, figsize=(12,5))
plt.show()
'''
두 분포간의 차이가 있으며 개별 분포를 봐도 count값 분포가 다르므로 y에 효과가 있음을 추론가능
'''

# scatter plot for some group
#temp를 추가해서 삼차원 그래프
raw_fe[raw_fe.workingday == 0].plot.scatter(y='count', x='Hour', c='temp', grid=True, figsize=(12,5), colormap='viridis')
plt.show()
raw_fe[raw_fe.workingday == 1].plot.scatter(y='count', x='Hour', c='temp', grid=True, figsize=(12,5), colormap='viridis')
plt.show()
'''
temp도 두 그래프의 분포가 다르므로 영향을 줄거라는 걸 추론 할수있다.
'''

# box plot example_날씨에 따른 수요 변화
raw_fe.boxplot(column='count', by='weather', grid=True, figsize=(12,5))
plt.ylim(0,1000)
raw_fe.boxplot(column='registered', by='weather', grid=True, figsize=(12,5))
plt.ylim(0,1000)
raw_fe.boxplot(column='casual', by='weather', grid=True, figsize=(12,5))
plt.ylim(0,1000)
'''
날씨에 따른 count 변화가 보인다.
'''


# box plot example_년도에 따른 수요 변화
raw_fe.boxplot(column='count', by='Year', grid=True, figsize=(12,5))
plt.show()
'''
년도에 따른 수요가 다르다는 걸 알수 있다. y에 영향을 준다
'''

# box plot example_월에 따른 수요 변화
raw_fe.boxplot(column='count', by='Month', grid=True, figsize=(12,5))
plt.show()

#독립변수간의 상관관계를 파악하기 위한 시각화
#상관관계를 추정하는게 알고리즘의 목표
pd.plotting.scatter_matrix(raw_fe, figsize=(18,18), diagonal='kde')
plt.show()

- 색깔이 짙을수록 관계성이 강하다는 의미
# selecting of columns from correlation tables
#y값과 x들 간의 상관관계 보기
'''
아래 값이 회귀분석 결과에 나온 계수값과 비슷한지 비교해봐야 한다
유사하지 않기 때문에 t검정이 유의하지 않다고 한것이다.
count_lag2 회귀분석결과를 비교해도 다름을 알수있다.
'''
raw_fe.corr().iloc[:,8:11]

# correlation table example
raw_fe.corr().iloc[0:8,8:11].style.background_gradient().set_precision(2).set_properties(**{'font-size': '15pt'})
검증지표 방향
R-squared(R^2):추정된 (선형)모형이 주어진 데이터에 잘 적합된 정도, 계량경제학에서는 모델에 의해 설명되는 데이터 분산의 정도(퍼센트)
R-squared는 기준이 ybar이다. 이는 다른 mse,mae와 차이점이다.
-> 평균적으로 추정된 값보다 얼만큼 잘 적합이 되었는지 확인
최소값은 마이너스 무한대이다.

Mean Absolute Error(MAE): 각 데이터의 단위를 보존하는 성능지표
단위보존 ? mse와 비교하면 알수있다.
Mean Squared Error(MSE): 가장 많이 사용되며 큰 오차에 패널티(Penalty)를 높게 부여하는 성능지표
mse는 실제값-예측값의 제곱이므로, 0보다 작은값은 더 작게, 1보다 큰 값은 더 크게 만들고 애초에 y값 자체의 스케일이 클수도, 작을수도 있다.
mae는 절대값으로 이뤄져 있기 때문에 작은 값이 더 작게, 큰 값은 더 크게 계산되지 않는다
즉, mae는 y스케일을 그대로 보존할수 있다.
Summary

- Squared 가 들어간 평가지표는, 이상치 하나만 있어도 오차가 제곱이 된다. 훨씬큰 오차가 반영됨
따라서 이상치가 있다면 yes로 표기된 평가지표를 쓰기를 추천
편향, 분산 상충관계
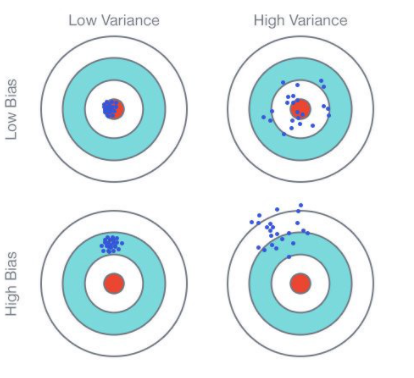
*bias를 보는건 train학습이 잘되었는지(과적합인지 아닌지) 확인할때 본다
편향이 작다면 정확성가 높고 (오버핏팅)
편향이 크다면 정확성이 낮다 (언더핏팅)
*분산을 보는건 test 데이터에 대해서 정확성이 안정적으로 나올지 아닐지를 확인할때 본다
분산이 작다면 다른 데이터로 예측시 적은 변동 예상
분산이 크다면 다른 데이터로 예측시 많은 변동 예상
*이둘의 관계그래프를 보면 모델이 복잡할수록 값이 증가한다.
왜일까? 모델이 복잡할수록 train 데이터에 과적합이 되고(bias 증가), 새로운 test 데이터가 들어올때
어디로 튈지 모르게 되므로 분산값이 커진다.(variance 증가)
분산과 편향을 둘다 줄여야 오류가 작아진다
'Data Diary' 카테고리의 다른 글
| 2021-03-18(시계열데이터 심화5_현실성을 반영한 데이터패턴& Scaling) (0) | 2021.03.18 |
|---|---|
| 2021-03-17(시계열데이터 심화4_잔차진단) (0) | 2021.03.17 |
| 2021-03-15(시계열데이터 심화2_FE&Data split) (0) | 2021.03.15 |
| 2021-03-13(Opencv 복습) (0) | 2021.03.13 |
| 2021-03-12(시계열데이터 심화1) (0) | 2021.03.12 |


