*본 내용은 시계열데이터 강의 내용 중 일부분을 요약한 내용입니다
정규화 방법론(Regularized Method, Penalized Method, Contrained Least Squares)
-선형회귀 계수(weight)에 대한 제약 조건을 추가함으로써 모형잉 과최적화를 맏는 방법
정규화 회귀분석이 왜 필요하는걸까?? 이 개념이 왜 등장 한 걸까?
아래 처럼 세가지 모델이 있다고 가정하자

이 중에서 어떤 모델이 가장 좋은 걸까? 라는 생각에서 시작이 해봅니다. 위 모델들을 아래 그래프로 설명하자면

1번 모델은 왼쪽 실선 박스에 해당하고 3번 모델은 오른쪽 회색 실선 박스에 해당됩니다. 1번은 train,test 둘다 에러가 높고 3번모델은 train에 아주아주 잘 적합이 되어서 train error는 작게 나옵니다. 그치만 정작 test error는 점점 높아집니다. train의 bias가 0에 가깝게 나왔지만 variance가 엄청 높게 나와서 test 성능이 나쁘게 나오게 된겁니다.
쉽게 생각하자면 시키는 일만!! 잘하는 사람입니다. 회사생활할때는 말하지 않아도, 시키지 않아도 해야하는 일들이 있는데 오른쪽 회색 박스에 있는 사람들은 훈련된 일만, 시키는 일만! 잘하고 다른건 일절 못하는 사람이라고 봐도 될것같습니다. 이럴거면 차라리 업무는 조금은 못하더라도 알아서 할줄 아는 사람이 훨씬 유능하다는 소리를 듣기 마련이죠.
이와 마찬가지로 train으로 훈련할때 어느정도 일반화에 가깝게 훈련을 진행해야 합니다. 따라서 train 성능이 좀 나빠지더라도 test 성능이 개선되는 편이 올바른 방향입니다. 3번 모델이 2번 모델로 만들어야 올바른 방향인데 이때 사용되는 것이 정규화 회귀분석입니다.
1) Ridge Regression


빨간색 밑줄이 추가된 부분입니다. 이 부분을 최소화 하는 값을 찾는다는 의미입니다.
아래 이미지에 나온 식이 있는데 이 전체 값이 가장 적은 숫자가 나오기 위해서는 어떻게 해야 할까요?
5000이라는 큰 값이 있어서 베타가 1만 나와도 큰 값이 더해집니다. 이 전체 값을 가장 적게 만들기 위해서는 베타가 0에 가까운 값, 예를들어 소수점 여야 합니다. 이런 식으로 베타 값에 제한을 줄수 있습니다. 그래서 책에서는
람다 값이 커지면 정규화 정도가 커지고 가중치 베타는 커질수 없다. 작아진다 라는 얘기가 나오게 된 것입니다.
만일 5차식의 복잡한 모델이 있다고 가정할때, 람다값을 10000을 주게 되면 베타 값들은 거의 0으로 떨어지고 남은건 상수인 베타제로 만 남게 될것입니다. 즉 5차식이 상수가이를 언더 핏팅이라고 합니다.
반대로 람다값이 제로에 가까운 값을 주게되면 제약이 미미하기 때문에 베타값이 다 살아나서 5차식이 그대로 사용됩니다. 여기서 정규화 정도라는 것은 "제약을 주었다",'혼란스러운 모델을 정리해 주었다' 정도의 의미가 이해하기 좋습니다
큰 숫자가 나오지 못하도록 제한을 한다는 의미를 다시 한번 생각해 볼 필요가 있습니다.
어떤 회귀분석 결과의 계수값들이 말도 안되게 큰 단위로만 구성이 되어 있다고 할때 릿지를 통해서 베타(계수값)를 줄인다면 이는 스케일링 효과도 내포함을 알수 있습니다. 상식적으로 불가능한 큰 계수를 조금 더 현실성 있는 값으로 변환 해줄수 있게 되는 겁니다.
2) Lasso Regression
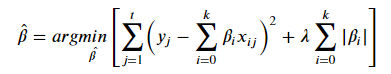
이번에는 절대값이 제약을 가하게 되면 0에 수렴하게됩니다. 아래 그래프를 보면서 왜 0인지 설명하겠습니다.

절대값은 제곱 형태와 달리 마름모 형태로 그래프가 생성이 됩닌다. 여기서 mse인 타원형과 만나는 지점을 보면
w1=0입니다. 다시말해서 Y값에 영향을 주지 못하는 것들은 0으로 만들어 버리는 것이 lasso입니다.
람다를 점점 더 크게 줄 수록 제거 되는 베타 값들이 늘어 나게 됩니다.
3) Elastic Net
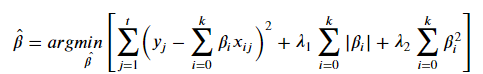
Lasso 식에서 Ridge의 제약 형식이 추가가 된 형태입니다. 큰 개념은 상관관계가 높은 변수의 계수는 같은 값으로 생각하겠다는 것입니다. 즉 중요하면 똑같이 중요하다 라고 하고 중요하지 않다면 똑같이 중요치 않도록 판별하겠다는 의미입니다. 저도 이 부분에 대해서는 좀더 공부가 필요해 보입니다. 완벽히 이해를 하지 못했습니다 ㅠ
앙상블 모델
오늘 앙상블 모델 강의에서 무릎을 탁치는 순간이 있었습니다. 먼저 배깅의 무릎 탁 순간을 말씀드리겠습니다
1. 배깅
배깅은 샘플을 여러번 뽑아서 각 모델을 학습시켜 결과를 집계(Aggregration)하는 방법입니다.여기서
무릎 탁 순간은 이 배깅이 중심극한정리의 원리와 매우 흡사하다는 점이 였습니다.
중심극한정리는 각 샘플에서 나온 통계량 값을 다시 평균을 취하면 모집단을 대표한다는 이론입니다. 이론만 봐도 이 둘이 매우 흡사 하다는 점입니다.
배깅 중 랜덤포레스트는 배깅의 마지막 과정인 취합 부분에서 평균을 내는것이 아니라 가장 예측 값이 잘 나온 것을 대표로 선정합니다.
2. 부스팅
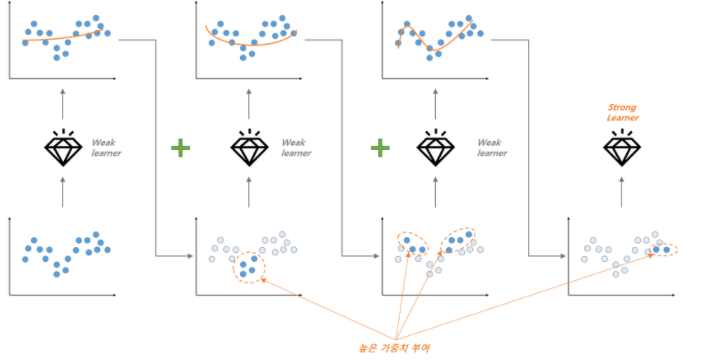
부스팅은 여러 모델들(weak learner)을 만들고, 이들을 합쳐서 하나의 stronger learner로 만듭니다.
과소적합된 부분에 가중치를 높혀서 적합한 모델로 만드는 과저인데, 과소적합된 부분을 판별하는 기준은 잔차입니다. 잔차가 크면 이를 줄이기 위해서 모델이 변하게 됩니다. 여기가 무릎 탁 순간입니다. 부스팅 원리는 잔차진단과 비슷합니다. 즉 잔차에 남아 있는 패턴들을 소거해 나간다는 큰 개념이 일치 합니다.
*마무리 하면서
이번 포스팅에서는 실습 코드 내용보다는 이론에서 많은 걸 얻었던 내용이라서 글 위주로 적었습니다
적은 내용들 보면 간단한 것같은데 저 내용들을 깨닫기 까지의 시간이 생각보다 오래 걸렸습니다. 저처럼 같은 부분에서 막혔거나 하시는 분들에게 많은 도움이 되었으면 합니다
'Data Diary' 카테고리의 다른 글
| 2021-03-29(시계열데이터 심화9_ARMR&ARIMA) (0) | 2021.03.29 |
|---|---|
| 2021-03-24(시계열데이터 심화8_Y의 정상성변환) (0) | 2021.03.24 |
| 2021-03-20 기록 (0) | 2021.03.20 |
| 2021-03-19(시계열데이터 심화6_다중공선성 제거&정상성) (0) | 2021.03.19 |
| 2021-03-18(시계열데이터 심화5_현실성을 반영한 데이터패턴& Scaling) (0) | 2021.03.18 |


