*본 내용은 시계열데이터 강의 내용 중 일부분을 요약한 내용입니다
개요
오늘은 시계열 딥러닝에 대한 내용을 포스팅합니다.
시계열 딥러닝은 구간추정값 없이 오직 점추정값을 출력하고 연산과정에서의 설명력이 떨어지므로 신뢰성이 낮다는 단점이 있습니다. 그런데도 불구하고 시계열 딥러닝을 이용하는 이유는 뭘까요? 대략 세가지의 장점이 있습니다.
1. Feature Engineering을 자동으로 구해줍니다.
히든레이어를 통해서 데이터 안에 숨겨진 패턴을 찾아낼 수 있습니다. 히든레이어의 층이 깊어 질수록 1차,2차,3차 쭉죽 늘어나게 됩니다. 그래서 3차식에서 알수 있는 특징이 있고, 4차식에서 알수 있는 특징을 찾아 낼수 있습니다.
2. 입력& 출력의 자유도 높습니다.
입력을 어떻게 줄건지, 출력은 어떤 형태로 할건지 사용자가 정할수 있는 자유도가 있습니다.
3. 시퀀스 길이를 제한없이 다양한 패턴으로 적용할수있다.
시퀀스길이를 사용자 마음대로 조절이 가능합니다. 4일치 데이터로 미래를 예측할건지 60일치 데이터로 예측할건지 정할수가 있다는 거죠 게다가 높은 정확도도 딥러닝을 사용 할수 밖에 없는 이유 중 하나입니다.
본격적으로 시계열 딥러닝의 알고리즘에 대한 소개를 하겠습니다.
Recurrent Neural Network: RNN
입력층 > 은닉층 > 출력층으로 연결된 단방향 신경망 외에 이전 출력값이 다시 입력으로 연결되는 순환신경망



RNN은 AR을 적용한 딥러닝 버전입니다. AR은 자기 자신의 이전 값을 입력으로 사용합니다. 이와 마찬가지로 RNN도 자기 자신의 이전의 값을 가져오는데, 여기서 차이점은 AR은 데이터를 가져오고 RNN은 히든레이어 정보를 가져옵니다.
왜 차이가 나는걸까요? RNN의 입력값은 batch사이즈 만큼 들어옵니다. 따라서 매번 층을 돌릴때마다 데이터를 누적시키는건 상식적으로 생각해도 비효율적입니다. 이 batch사이즈 만큼 들어온 데이터를 대표할 만한 값이 있어야 하는데 이를 히든레이어가 합니다. 히든레이어에 데이터의 특징 정보가 있기 때문에 다음 히든레이어를 계산 시 함께 연산하면 됩니다. 위 이미지를 보면 녹색 동그라미가 이에 해당됩니다. 주황색의 f() 는 비선형으로 만들어 주는 활성함수 입니다.

역전파(Backpropagation Through Time: BPTT)
앞으로 전진하는 Feed Forward Network(FFN)과 달리 각 시점마다 Loss Function에서 추정된 Error를 이전 시점으로 전파함
공통 파라미터: 각 시점마다 출력 희망값(Y^)과 실제 출력값(Y)의 Error로 가중치(w)들을 업데이트 함
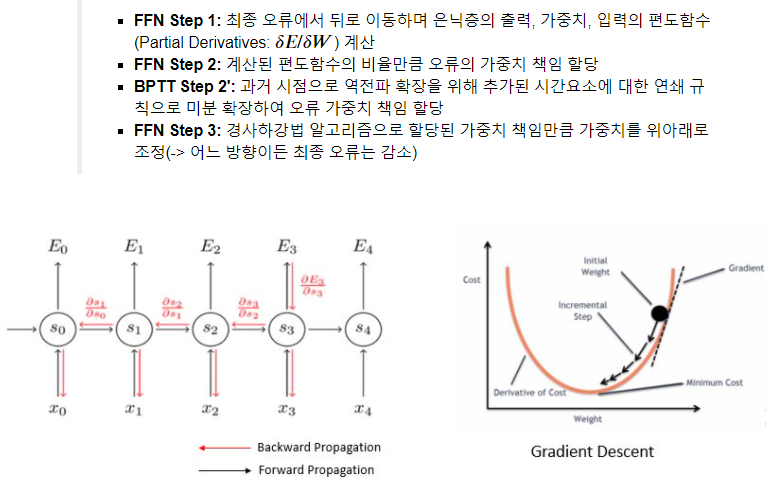
역전파를 사용해서 가중치를 업데이트 할수 있습니다. 하지만 이는 또 다른 문제를 야기 시킵니다. 저번 포스팅에서 언급했었듯이 미분은 곱셈의 연산이 있기 때문에 0.5 *0.5 = 0.25 가 되는 것처럼 점점 값이 작아져서 잔차가 0이 됩니다.
그렇기 때문에 전파가 되는 양이 점점 작아지는 문제가 생깁니다.

LeRu를 사용을 지양하는 이유
-> RNN계열은 이전 값들이 사용되므로 한번 0으로 빠지면 이전 정보가 손실이 되기때문에 tanh를 여전히 사용한다
Long Short-Term Memory: LSTM

곱하기로 인한 정보 손실을 막고자 덧셈을 이용한 알고리즘입니다.

C라는 기억셀을 추가하여 이를 바탕으로 외부 계층에 은닉상태 H를 출력합니다. C는 LSTM 계층 내에서만 전달되며 과거부터 t까지 모든 정보 저장됩니다.

Ft = sigmoid(새로운 X데이터* 가중치 W + 이전 히든레이어의 정보값*가중치 U)
이 Ft에다가 이전의 모~든 정보를 기억하고있는 Ct-1를 곱해 줌으로써 정보를 잊게 합니다.




정리: RNN은 시간이 지나면 이전 값을 잊어버리는 반면, LSTM은 각 게이트를 통해 이전 입력값이 계속 저장되어 필요한 시점에 출력 및 반영됨
장기기억셀(C)는 덧셈으로 되어있기 때문에 곱셈에 의해 작아지는 전파력이 감소하지 않게 됩니다.
Gated Recurrent Unit: GRU
LSTM보다 구조를 간결하게 만들어서 빠른속도와 유사한 성능을 보입니다.
변경된 점
1. LSTM의 Gate 3개 -> GRU Gate 2개
: Reset Gate & Update Gate(LSTM의 Forget+Input과 유사)
2. Output Gate가 없는 LSTM이기에 메모리셀에 담기는 정보 양 증가
3. LSTM의 Ct와 Ht가 하나의 벡터 Ht로 통합
4. GRU가 LSTM보다 학습할 가중치가 적어짐



업데이트를 관장하는 U는 새로운 데이터의 정보를 얼만큼 반영하느냐를 정합니다.
1-U는 위 설명처럼 얼마나 잊을지 결정하는데, U가 1이면 (새로운 입력정보를 모두 사용하겠다) ht 게이트는 작동을 할 것이고 forget을 담당하는 1-U는 0 이 되므로 기능을 발휘 하지 못합니다. 즉 잊을 부분이 없다는 겁니다. U을 구성요소를 보면 이전 히든레이어값이 들어 있습니다. 이 히든레이어에 t-1정보가 있을것입니다. 따라서 과거 정보와 현재 입력으로 들어가는 정보를 모두 사용한다면 1이 될것이고, 버릴 부분이 없다는 의미로 1-U =0이 되어서 forget할 부분이 없다는 의미 입니다.
만일 U의 비율이 0.5라면 어떤 해석이 가능할까요
U에서는 sigmoid(새로운 정보+이전 정보)의 결과가 0.5 이므로 새 정보+ 이전 정보에서 절반은 반영하고 절반은 버린다는 의미로 해석될것입니다. 이때 ht는 절반만 들어간 U * reset gate + 새로운 정보
절반이 남은 1-U는 ht-1과 곱해집니다. 만일 1-U상태로 출력이 된다면 vanishing Gradients 문제는 해결되지 않습니다.
왜냐면 다음 t+1 시점에서 또 forget이 작동하기 때입니다. 따라서 새로운 정보를 '더하기' 해줘야 하는데 이때 ht로 더해줍니다.

'Data Diary' 카테고리의 다른 글
| 2021-04-15(시계열데이터 심화19_종강1) (0) | 2021.04.15 |
|---|---|
| 2021-04-14(시계열데이터 심화18_bitcoin 실습편) (0) | 2021.04.14 |
| 2021-04-12(시계열데이터 심화16_딥러닝) (0) | 2021.04.12 |
| 2021-04-10 기록(시계열 데이터 심화_비선형 복습) (0) | 2021.04.10 |
| 2021-04-09(시계열데이터 심화15_비선형 알고리즘) (0) | 2021.04.09 |
