Chain Rule

위 두 함수가 있을때 이를 결합한 Z함수가 아래처럼 있습니다.

이때, Z함수를 s로 미분한 값을 알아 낼수 있을까요? S는 X,Y에 포함된 element입니다.
그리고 X,Y는 Z함수안에 포함되어 있습니다. 흐름을 보면 Z함수-X,Y함수-s,t elements 이렇게 관계가 맺어져 있습니다.
이게 무슨 뜻일까요? 이 관계를 한번 들여다 보겠습니다.
Z라는 함수가 바닷물이고 그 바닷물 안에는 X,Y함수라는 물고기가 있고 s,t는 물고기가 잡아 먹은 먹이 같은 구조입니다.
음.. 딥러닝이 가능한 이유는 Back propagation이 있기 때문입니다. 다시말해서 오차를 쪼개서 파라미터를 업데이트해줄때 사용되는게 이 체인 룰입니다.
이 바닷물의 수질을 아주 깨끗하게 만들고 싶습니다. 오염도가 2정도 나오면 좋겠는데, 결과는 10이 나와서
오차가 8이라는 결과를 얻었습니다. 이 8을 쪼갭니다. 각 파라미터들에게 나눠줘서 오차를 줄이는 방향으로 만듭니다.
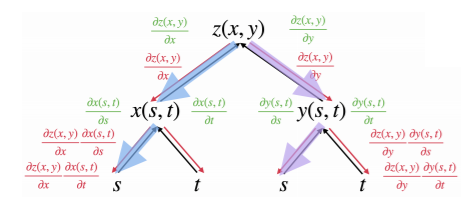
초록색은 X,Y -> Z로 올라가는 과정(forward propagation)
빨간색은 Z -> X,Y로 내려가는 과정(Back propagation)
이때 S라는 먹이감의 변화에 따라서 바닷물의 수질에 얼만큼 영향을 주는지 궁금할수 있습니다.
S 먹이감이 만일 독극물이라면 그걸먹은 물고기가 바닷물 수질에 악영향을 줄수도 있을것입니다.
반대로 정상적인 먹이라면 깨끗한 수질을 만드는데 최소한 악영향은 주지 않을 것입니다.
그래서 우리는 S라는 먹이감 변화에 따른 바닷물 수질 변화량을 알아야 합니다. 이를 구하기 위해서 체인룰이 사용됩니다. 빨간색 미분값을 보면 그 정답을 알수 있습니다.

파란색 미분값은 파란색 화살표가 그려진 미분값입니다. 보라색은 보라색 화살표 미분값입니다.
forward propagation 할때 이미 미분값을 구해 놨으므로 back propagation할때는 저장해놓은 미분값을 곱하기만 하면 됩니다. 그래서 연산이 빨라지고 딥러닝이 가능해 지는것입니다.
위 식은 S 먹이감 변화에 따른 수질의 영향을 알기 위한값입니다. 따라서 X 물고기가 먹은 S먹이감 + Y물고기가 먹은 S먹이감 이 둘을 더해서 구할 수 있었습니다.
Vector Chain Rule은 위 예시의 스칼라값 대신 벡터 or 매트릭스가 들어가는 형태입니다. 예시를 들자면

위 처럼 각 함수 값이 스칼라가 아닌 백터 형식으로 되어있고 마지막 Z함수는 X+Y를 한 후 1/n으로 나눈 평균값 스칼라가 되겠습니다. 먼저 forward propagation이 실행되므로 각 element로 미분한 값은 아래와 같습니다.



그리고 스칼라 체인룰와 같은 방법으로 back Propagation을 해주면 됩니다.


위 예시로 계산하면 마지막 결과 shape는 1*n 벡터입니다. 계산을 꼭 해봐야 shape를 알수 있는 것은 아닙니다.
m개의 f함수와 n개의 element가 있을때의 자코비안 shape은 m*n입니다. 이것을 이용하면
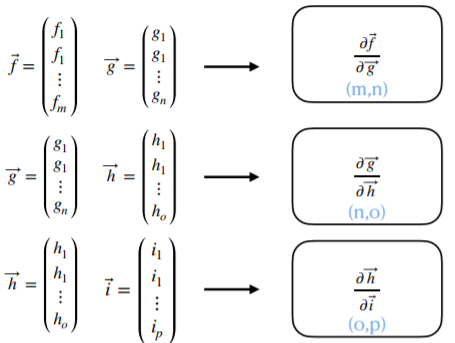
계산하기 전에 shape를 추정해 볼수 있게 됩니다. 결국 최종적으로 가장 아래에 있는 i(먹이) element와 바닷가 수질을 나타내는 f함수의 미분을 구했을때의 shape를 추정해 볼수 있게 됩니다.

좀 더 구체적으로 보면

위 식을 보면 chain처럼 연결고리가 있다는 걸 직관적으로 알수가 있습니다.
따라서, 딥러닝의 back propagation은 위 식의 순서대로 오차를 뿌려준다고 생각하면 될것같습니다.
'Data Diary' 카테고리의 다른 글
| 2021-04-28(딥러닝수학4_Linear Regression & Gradient Descent) (0) | 2021.04.28 |
|---|---|
| 2021-04-27(태양열 에너지 예측2) (0) | 2021.04.27 |
| 2021-04-23(태양열 에너지 예측) (0) | 2021.04.23 |
| 2021-04-22(딥러닝 수학2_Gradient & Jacobian) (0) | 2021.04.22 |
| 2021-04-20(딥러닝 수학1) (0) | 2021.04.20 |


