딥러닝 연산 시 필요한 기본적인 노드들을 만들어 보면서 복습하는 시간을 가졌습니다.
아래의 노드들을 차례대로 생성해 줍니다.

1) Plus_node

x,y 를 더해서 z를 만들어 줍니다. z= x+y 를 각각 편미분하면 1이 나오고, 이를 체인룰을 통해
back propagation하면 위와 같이 차례대로 곱해 줄수 있겠습니다.
import numpy as np
class plus_node:
def __init__(self):
# x+y = z
self._x, self._y = None,None #arg를 새로 받을 것이기 때문에 none으로 설정
self.z = None
def forward(self, x,y):
self._x,self._y= x,y
self._z = self._x + self._y
def backward(self, dz): #dz -> 라운드J / 라운드z, 편미분값을 dz로 표현(편의성을 위해)
return dz,dz #각자의 편미분 1 * dz =dz 의 값을 x,y에 return 해줍니다.
2) minus_node

z = x -y의 편미분 결과 각각 1,-1이 나왔고 이 값은 back propagation 연산 시 곱해주게 됩니다. (위 빨간색 부분)
class minus_node:
def __init__(self):
# x-y = z -> 라운드z/라운드x =1, 라운드z/라운드y = -1
self._x, self._y = None,None
self.z = None
#forward propagation
def forward(self, x,y):
self._x, self.y =x,y
self._z = self._x - self.y
return self._z
def backward(self, dz):
return dz, -1*dz
3) Multiplication_Node
z = x * y의 편미분 값은 x는 y값을 갖고, y는 x값을 가지게 됩니다.

class mul_node:
def __init__(self):
self._x, self._y = None,None
self._z = None
def forward(self, x,y):
self._x, self._y = x,y
self._z = self._x * self._y
return self._z
def backward(self, dz):
return self._y*dz, self._x*dz
4) Square_Node
입력이 x 하나이고, 제곱인 형태를 구현합니다. z = x*x의 편미분은 2x입니다.

class sqare_node:
def __init__(self):
self._x = None
self._z = None
def forward(self, x):
self._x = x
self._z = self._x*self._x
return self._z
def backward(self, dz):
return dz*2*self._x
5) Mean_Node
입력은 x가 n개이고 z는 x들의 평균을 구한 값입니다. 각각을 편미분 하면 n개 만큼 각각 나눈값이 됩니다. 아래 이미지통해 확인할수 있습니다.

class mean_node:
def __init__(self):
self._x = None
self._z = None
def forward(self, x):
self._x = x
self._z = np.mean(self._x)
def backward(self, dz):
print(len(self._x)) #5
print(1/len(self._x)) #0.2
print(np.one_like(self._x)) #[1. 1. 1. 1. 1.] #5개 길이 만큼 1로 채운다
print(1/len(self._x)*np.one_like(self._x)) #[0.2 0.2 0.2 0.2 0.2], 1/n에 대한 array를 만듦
dx = dz*1/len(self._x)*np.one_like(self._x) # [0.4 0.4 0.4 0.4 0.4]
return dx Single-variate Linear Regression without Bias Term for a Single Sample: 이론편
Iteration의 개념

위 예시에는 특정 포인트의 loss값에 대한 세타 값을 업데이트하는 과정입니다. iteration은 세타를 업데이트시키는 기준이 됩니다.
- 세타를 한번 업데이터 = 1teration
- n개의 포인트를 가지고 cost를 구한 뒤 세타를 업데이트 = iteration
Epoch의 개념

len(x_data)의 길이가 백개든 천개든 모든 세타를 전체 한번씩 업데이트 시킨 것을 1epoch라고 합니다.
Model/Loss Setting

위 식을 forward, backward 이론식으로 표현한다면 아래와 같습니다.
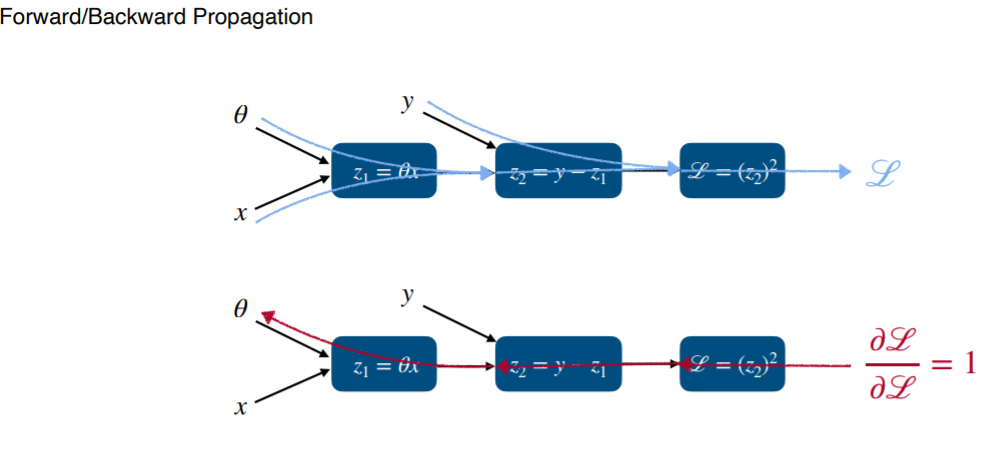
z1 = 세타x는 y^와 같습니다. z1을 구해준뒤 z2로 넘어가면서 실제 값 y를 받아서 loss값을 구하게 됩니다.
backward할때는 세타만 업데이트가 되므로 세타 방향으로만 뻗어가게 됩니다.
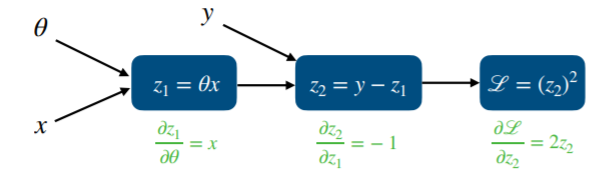
각각의 편미분을 구한 값입니다. 이는 bw할때 아래처럼 사용됩니다.
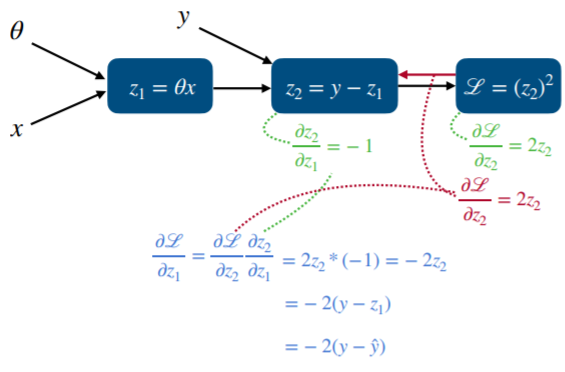
라운드L/라운드z1의 값을 구하기 위해서는 위 식 처럼 각각 단계의 편미분값을 차례대로 곱해줍니다. 이 곱해진 값은
최종적으로 업데이트 시킬 세타값을 구하기 위해 사용됩니다. 참고로 z2 = y- z1인데 z1은 y^과 동일합니다.
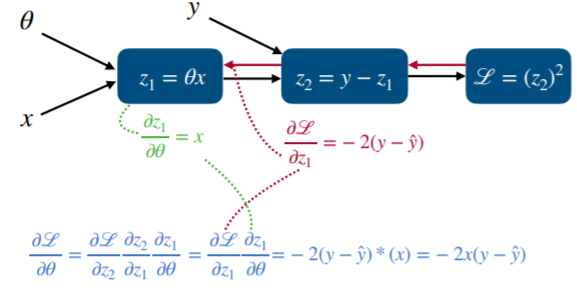
최종적으로 세타에 전달되는 편미분 값은 -2x(y-y^) 입니다. 아래 이미지로 정리를 해봅니다.
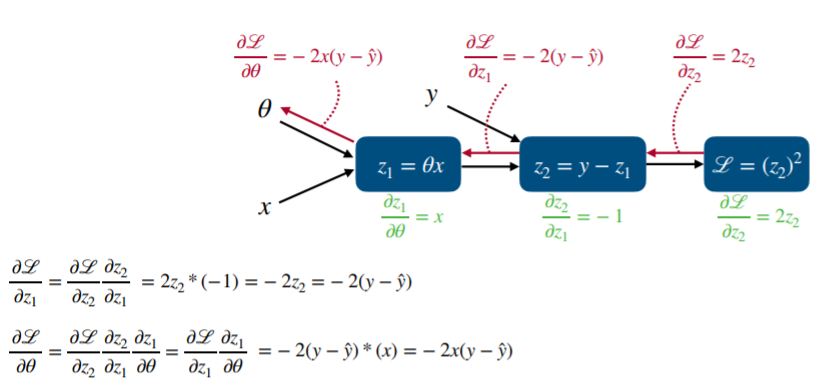
이러한 값을 통해 학습을 진행할텐데 어떤 수식으로 정리 할수 있을지 아래를 통해 확인해 보겠습니다.
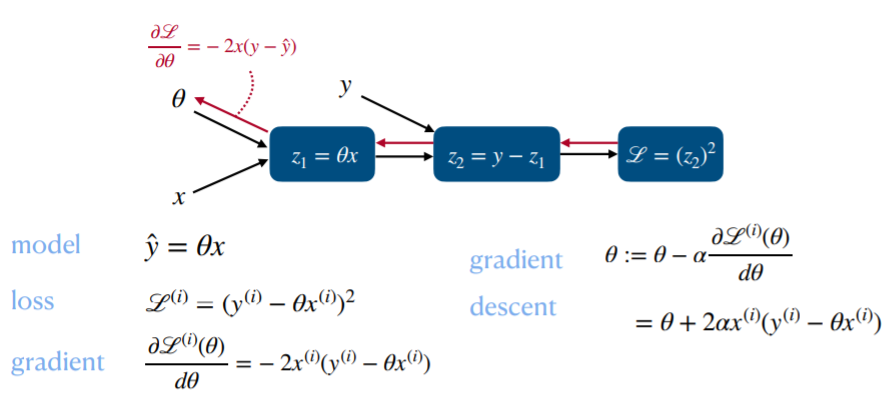
model - loss - gradient 까지 구한 다음에 학습을 진행하게되면 오른쪽 gradient descent 와 같은 모습을 보이게 됩니다.
달라진 점은 gradient의 음수 값과 학습률 알파가 접목된 것이 gradient descent입니다. 마이너스와 알파 값의 변화에 따른 학습이 어떻게 진행 되는지 알아보겠습니다.

각 변수의 변화는 위와 같이 나타낼수 있습니다.

실제값이 예측값보다 큰 경우
1) x>0 일때
2ax(y_y^) 자체가 양수가 되므로 기존의 세타에 추가적인 값이 더해지므로 y^가 조금 더 커져서 y와 비슷해지는 방향으로 학습합니다.
2) x<0 일때
-2ax(y_y^)이 되므로 기존의 세타에서 조금씩 감소하게 된다. 여기서 중요한 점은 y^ = 세타 * x 에서 x는 음수라는 점이다 예를들어 세타가 5,4,3,2,1 순으로 업데이터가 되었다면 y^ = -5,-4,-3, ... 순으로 값이 커지게 될것이다. 최종적으로 실제 y 와 비슷해지는 방향으로 학습이 된다.

위 이미지에서 값이 점차 커져서 올바른 방향으로 학습되어가는 과정이라고 볼수 있다.
실제값이 예측값보다 작은 경우

예측값이 크다면 이를 y방향으로 줄어야 한다. (y-y^은 음수이다)
1) x>0 일때
2ax(y-y^)은 음수이므로 세타를 점차 감소시킨다. 또한 y^= 세타*x 도 점차 감소하게 된다. 따라서
y-세타*x 는 점차 줄어들게 될것이다.
2) x<0 일때,
2ax(y-y^)에서는 음수 * 음수가 만나서 양수가 되므로 세타값이 점차 커지게 된다.
점차 커지는 세타는 y^ = 세타 * x 에서 x(음수)를 만나서 점차 작아지는 값으로 바뀌게 된다.
따라서 y-y^의 값도 점차 작아지게 된다.
'Data Diary' 카테고리의 다른 글
| 2021-05-22(태양열 에너지 예측10) (0) | 2021.05.22 |
|---|---|
| 2021-05-19(태양열 에너지 예측9) (0) | 2021.05.19 |
| 2021-05-17(태양열 에너지 예측8) (0) | 2021.05.17 |
| 2021-05-15(태양열 에너지 예측7) (0) | 2021.05.15 |
| 2021-05-14(태양열 에너지 예측6) (0) | 2021.05.14 |


