반응형
*본 내용은 시계열데이터 강의 내용 중 일부분을 요약한 내용입니다

저번 포스팅에서 분석 사이클을 대략적으로 정리 했는데 강의자료에 깔끔하게 나와 있어서 가져왔습닌다
아래실습을 통해 어떻게 적용 하는지를 알아 볼수 있었습니다
실습: 항공사 승객수요 Auro-ARIMA 모델링
# 라이브러리 호출
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
%reload_ext autoreload
%autoreload 2
from module import stationarity_adf_test, stationarity_kpss_tesst
#데이터 준비
data= sm.datasets.get_dataset("AirPassengers")
raw=data.data.copy()
#데이터 전처리
##시간 인덱싱
if 'time' in raw.columns:
#time컬럼 길이 만큼 월로 바꾸기
raw.index=pd.data_range(start='1/1/1949', periods=len(raw['time']), freq='M')
del raw['time']
#정상성테스트
### 미변환(아~무것도 하지 않고 바로 정상성 확인하기->패턴&파라미터 등 파악
candidate_none= raw.copy()
display(stationarity_adf_test(candidate_none.values.flatten(),[])) #비 정상성
display(stationarity_kpss_test(candidate_none.values.flatten(), [])) # 비 정상성
sm.graphics.tsa.plot_acf(candidate_none, lags = 100, use_vlines=True)
'''
유의한 lag값들이 존재하며 계절성이 보인다.
대체로 하락하는 추세를 보인다.
'''
plt.tight_layout()
plt.show()
###로그 변환
candidate_trend= np.log(raw).copy()
display(stationarity_adf_test(candidate_trend.values.flatten(), []))
display(stationarity_kpss_test(candidate_trend.values.flatten(), []))
sm.graphics.tsa.plot_acf(candidate_trend, lags=100, use_vlines=True)
plt.tight_layout()
plt.show()
'''
크기는 줄었지만 비 정상성의 패턴은 여전히 남아 있다.
'''
trend_diff_order_initial=0
result = stationarity_adf_test(candidate_trend.values.flatten(),[]).T
if result['p-value'].values.flatten() < 0.1:
trend_diff_order = trend_diff_order_initial
else:
trend_diff_order = trend_diff_order_initial+1
print('Trend Difference: ', trend_diff_order)
### 로그+추세차분 변환(1회 진행)
candidate_seasonal = candidate_trend.diff(trend_diff_order).dropna().copy()
#adf 결과 비 정상성 이지만 0.07로 상당히 줄었다.
display(stationarity_adf_test(candidate_seasonal.values.flatten(), []))
display(stationarity_kpss_test(candidate_seasonal.values.flatten(),[])) #정상성
#튀는 값과 반복되는 계정성 패턴이 여전히 보인다. 계절성 차분이 필요해 보임
sm.graphics.tsa.plot_acf(candidate_seasonal, lags=50, use_vlines=True)
plt.tight_layout()
plt.show()
seasonal_diff_order =sm.tsa.acf(candidate_seanal)[1:].argmax()+1 #계절성m 추출
print('Seasonal Difference: ', seasonal_diff_order)
###로그+추세차분+계절차분 변환
candidate_final = candidate_seasonal.diff(seasonal_diff_order).dropna().copy()
display(stationarity_adf_test(candidate_final.values.flatten(), []))
#둘다 정상성을 보이고 있다.
display(stationarity_kpss_test(candidate_final.values.flatten(), []))
sm.graphics.tsa.plot_acf(candidate_final, lags=100, use_vlines=True)
#lag1,3,12에서 자기상관이 검출 되었지만 최소한 추세와 계절성 패턴은 사라졌다
plt.show()








## 최종 타겟 선정 및 Train/Test 데이터 분리
candidate = candidate_trend.copy()
split_date = '1958-01-01'
Y_train = candidate[condidate.index < split_date]
Y_test = candidate[candidate.index >= split_date]
## 시각화 및 모수추론(p=1, q=0, d=1, P=1, Q=1, D(m)=12)
'''
q=0, ACF 그래프만 보면 많은 q가 필요 할것같지만 일단은 차분이 있기 때문에 지금은 고려치 않는다
PACF에서 lag1이 튀었기 때문에 AR(1)
ACF의 lag12,24,36 값이 튀고 있다 Q=1(계절성 MA)
PACF에서 lag12 배수의 앞뒤 값도 함께 튄다 P=1(계절성 AR)
'''
plt.figure(figsize=(14,4))
sm.tsa.graphics.plot_acf(Y_train, lags=50, lapha=0.05, use_vlines=True, ax =plt.subplot(121))
sm.tsa.graphics.plot_pacf(Y_train, lags=50, alpha=0.05, use_vlines=True, ax=plt.subplot(122))
plt.show()
#SARIMA 모델링
logarithm, differencing =True, False
fit_ts_sarimax = sm.tsa.SARIMAX(Y_train, order=(1,trend_diff_order,0),
#계절성 차분 없는게 결론적으로 성능이 가장 좋았음
seasonal_order=(1,0,1,seasonal_diff_order), trend="c").fit()
display(fit_ts_sarimax.summary())
pred_tr_sarimax = fit_ts_sarimax.predict() # 점추정 값 출력
#점추정과 구간추정을 같이 볼려면 get_forecast -> y_test 길이 만큼 예측하기
#predicted_mean: 점추정 값을 output으로 출력
#confidence interval:신뢰구간
pred_te_ts_sarimax = fit_ts_sarimax.get_forecast(len(Y_test)).predicted_mean
pred_te_ts_sarimax_ci = fit_ts_sarimax.get_forecast(len(Y_test)).conf_int()
## 비정상성으로 변환
'''
위에서 추정된 점추장과 신뢰구간은 log가 된 Y값에 대한 수치를 추정한값이므로 환산할 필요가 있다
log의 역함수인 exponential를 취해준다
'''
if logarithm:
Y_train = np.exp(Y_train).copy()
Y_test = np.exp(Y_test).copy()
pred_tr_ts_sarimax =np.exp(pred_tr_ts_sarimax).copy()
pred_te_ts_sarimax = np.exp(pred_te_ts_sarimax).copy()
pred_te_ts_sarimax_ci = np.exp(pred_te_ts_sarimax_ci).copy()
#d입력값에 만일 차분이 들어가 있다면 차분의 역함수 격인 누적을 통해 오리지널값으로 변환
if differencing:
pred_tr_ts_sarimax = np.cumsum(pred_tr_ts_sarimax).copy()
#검증
%reload_ext autoreload
%autoreload 2
from module import *
Score_ts_sarimax, Resid_tr_ts_sarimax, Resid_te_ts_sarimx = evaluation(y_train, pred_tr_ts_sarimax,
Y_test,pred_te_ts_sarimax, graph_on=True)
display(Score_ts_sarimax)
ax = pd.DataFrame(Y_test).plot(figsize=(12,4))
pd.DataFrame(pred_te_ts_sarimax, index=Y_test.index, columns=['prediction']).plot(kind='line',
xlim=(Y_test.index.min(),Y_test.index.max()),
linewidth=3, fontsize=20, ax=ax)
ax.fill_between(pd.DataFrame(pred_te_ts_sarimax_ci, index=Y_test.index).index,
pd.DataFrame(pred_te_ts_sarimax_ci, index=Y_test.index).iloc[:,0],
pd.DataFrame(pred_te_ts_sarimax_ci, index=Y_test.index).iloc[:,1], color='k', alpha=0.15)
plt.show()
# 잔차진단
'''
잔차가 자유롭게 분포가 되어 있고 추세가 약간 있다.
분포는 아웃라이어가 하나 있지만 정규분포와 유사하다
ACF,PACF도 아웃라이어를 제외하면 WN과 유사하다
'''


- 계수들은 유의함
- Ljing-Box 결과 자기상관은 없는 걸로 판정
- jarque-bera 결과 정규분포로 판정
- 등분산성은 있는 걸로 판정
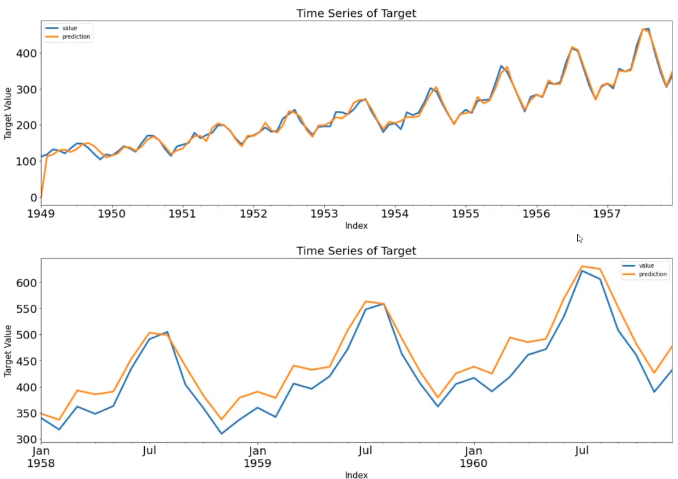

BikeSharingDemand_Auto_SARIMAX
for loop를 통해 SARIMAX의 자동화를 구현하는 실습내용입니다.
# Data Loading
# location = 'https://raw.githubusercontent.com/cheonbi/DataScience/master/Data/Bike_Sharing_Demand_Full.csv'
location = './Data/BikeSharingDemand/Bike_Sharing_Demand_Full.csv'
raw_all = pd.read_csv(location)
# Feature Engineering
raw_fe = feature_engineering(raw_all)
### Reality ###
target = ['count_trend', 'count_seasonal', 'count_Day', 'count_Week', 'count_diff']
raw_feR = feature_engineering_year_duplicated(raw_fe, target)
###############
# Data Split
# Confirm of input and output
Y_colname = ['count']
X_remove = ['datetime', 'DateTime', 'temp_group', 'casual', 'registered']
X_colname = [x for x in raw_fe.columns if x not in Y_colname+X_remove]
X_train_feR, X_test_feR, Y_train_feR, Y_test_feR = datasplit_ts(raw_feR, Y_colname, X_colname, '2012-07-01')
### Reality ###
target = ['count_lag1', 'count_lag2']
X_test_feR = feature_engineering_lag_modified(Y_test_feR, X_test_feR, target)
###############
### Scaling ###
X_train_feRS, X_test_feRS = feature_engineering_scaling(preprocessing.Normalizer(), X_train_feR, X_test_feR)
###############
### Multicollinearity ###
print('Number_of_Total_X: ', len(X_train_feRS.columns))
X_colname_vif = feature_engineering_XbyVIF(X_train_feRS, 12)
print('Number_of_Selected_X: ', len(X_colname_vif))
X_train_feRSM, X_test_feRSM = X_train_feRS[X_colname_vif].copy(), X_test_feRS[X_colname_vif].copy()
#########################
# 모델링
## Additional Features
# X변수가 포함된 모델링
# 랜덤 포레스트 중요도 12개 중 상위 7개 선정
exog_tr = X_train_feRSM[['count_seasonal', 'weather', 'count_lag2', 'count_diff', 'Quater_ver2', 'Hour', 'workingday', 'DayofWeek']]
exog_te = X_test_feRSM[['count_seasonal', 'weather', 'count_lag2', 'count_diff', 'Quater_ver2', 'Hour', 'workingday', 'DayofWeek']]
## Parameter Setting
p, q = range(1,3), range(1,3)
d = range(0,1)
P, Q = range(1,3), range(1,3)
D = range(1,2)
m = 12
trend_pdq = list(product(p, d, q))
seasonal_pdq= [(candi[0],candi[1],candi[2],m) for candi in list(product(P,D,Q))]
## SARIMAX
AIC = []
SARIMAX_order = []
#for loop를 통해 자동화
for trend_param in tqdm(trend_pdq):
for seasonal_params in seasonal_pdq:
try:
result = sm.tsa.SARIMAX(Y_train_feR, trend='c',
order = trend_params, seasonal_order=seasonal_params, exog=exog.tr).fit()
print('Fit SARIMAX: trend_order={} seasonal_order={} AIC={}, BIC={}'.format(trend_params, seasonal_params
,result.aic, result.bic, end='\r'))
AIC.append(result.aic)
SARIMAX_order.append([trend_param, seasonal_params])
except:
continue
## Parameter Selection
print('The smallest AIC is {} for model SARIMAX{}x{}'.format(min(AIC), SARIMAX_order[AIC.index(min(AIC))][0],
SARIMAX_order[AIC.index(min(AIC))][1]))
## Auto-SARIMAX Fitting
fit_ts_sarimax = sm.tsa.SARIMAX(Y_train_feR, trend='c', order=SARIMAX_order[AIC.index(min(AIC))][0],
seasonal_order=SARIMAX_order[AIC.index(min(AIC))][1], exog=exog_tr).fit()
display(fit_ts_sarimax.summary())
pred_tr_ts_sarimax = fit_ts_sarimax.predict()
#점추정
pred_te_ts_sarimax = fit_ts_sarimax.get_forecast(len(Y_test_feR), exog=exog_te).predicted_mean
#구간추정
pred_te_ts_sarimax_ci = fit_ts_sarimax.get_forecast(len(Y_test_feR), exog=exog_te).conf_int()
# 검증
Score_ts_sarimax, Resid_tr_ts_sarimax, Resid_te_ts_sarimax = evaluation_trte(Y_train_feR, pred_tr_ts_sarimax,
Y_test_feR, pred_te_ts_sarimax, graph_on=True)
display(Score_ts_sarimax)
ax = pd.DataFrame(Y_test_feR).plot(figsize=(12,4))
pd.DataFrame(pred_te_ts_sarimax, index=Y_test_feR.index, columns=['prediction']).plot(kind='line',
xlim=(Y_test_feR.index.min(),Y_test_feR.index.max()),
linewidth=3, fontsize=20, ax=ax)
ax.fill_between(pd.DataFrame(pred_te_ts_sarimax_ci, index=Y_test_feR.index).index,
pd.DataFrame(pred_te_ts_sarimax_ci, index=Y_test_feR.index).iloc[:,0],
pd.DataFrame(pred_te_ts_sarimax_ci, index=Y_test_feR.index).iloc[:,1], color='k', alpha=0.15)
plt.show()
#잔차진단
error_analysis(Resid_tr_ts_sarimax, ['Error'], Y_train_feR, graph_on =True)








반응형
'Data Diary' 카테고리의 다른 글
| 2021-04-03 기록 (0) | 2021.04.03 |
|---|---|
| 2021-04-02 기록(1차 방문) (0) | 2021.04.03 |
| 2021-03-31 기록 (0) | 2021.03.31 |
| 2021-03-30(시계열데이터 심화10_ARIMA&SARIMA) (0) | 2021.03.30 |
| 2021-03-29(시계열데이터 심화9_ARMR&ARIMA) (0) | 2021.03.29 |

