
우리가 원하는 포인트는 가장 최저점을 나타내는 global point이다. 하지만 위 그림처럼 local 포인트에 빠지거나, 평평한 부분인 saddle 포인트를 만나면서 최저점이라고 인식하는 오류를 범할수 있다. 이를 해결하기 위해 다양한 optimizer들이 등장했다.

주요 Optimizer들이다. momentum은 GD값을 조정하고, adagrad,rmsprop은 lr을 조정한다. adam은 GD,lr 모두 조정하면서 최적점을 찾는다.
*Momentum
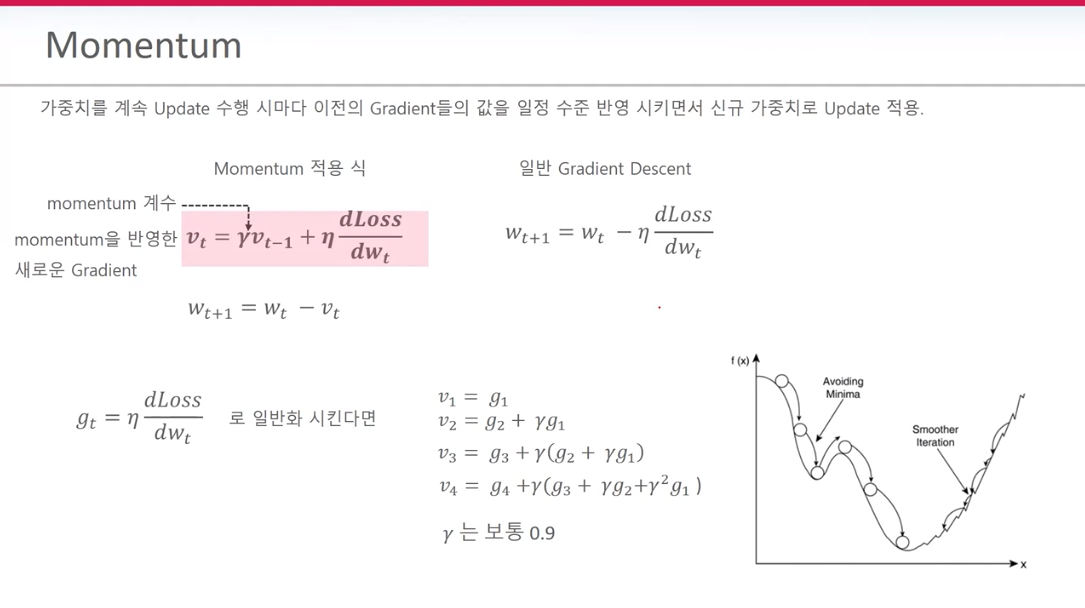
과거의 GD에 Momentum 가중치를 적용하여 새로운 GD를 계산한다. 기존의 GD는 wt+1 = wt- GD 이다. momentum은 이 GD에다가 감마라는 가중치를 적용해 준다. 헷갈리지 말아야 할점은 새롭게 구한 gradient에 감마를 곱하는게 아니다. 바로 이전에 구했던 GD에 감마를 곱한 뒤 새롭게 구한 GD에 더해준다. 식으로 표현하면
Wt+1 = 과거 GD - (새롭게 구한 gradient + 감마 * 과거 gradient)이다. GD는 gradient Descent이며 gradient와는 다른 값이다.
과거의 gradient을 감안하면 어떤 점이 좋은가?

현재 local 포인트에 갇혔다고 가정해 본다. 과거 gradient 두개 값을 더해주어서 local 지역을 빠져 나가게끔 힘을 보탤수가 있다.

각 입력되는 데이터의 크기에 따라 loss가 증감을 반복하기 때문에 SGD같은 경우엔 지그재그로 학습이 된다. 이럴경우 학습시간이 느려질뿐만 아니라 학습 자체가 안될수 있기 때문에 지그재그 학습 현상은 지양해야한다. momentum을 사용하면 이러한 지그재그 현상을 줄일수 있다.
*AdaGrad(Adaptive Gradient)

입력 데이터의 크기에 따라 각각의 가중치 학습속도에서 차이가 발생한다. 이때 AdaGrad를 활용하여 적게 학습된 가중치에는 lr을 크게 설정하고, 많이 학습된 가중치에는 작은 lr을 적용한다. 참고로, 각각의 가중치 학습 속도가 다를 경우 최적점에 도달하기엔 한계있다.
식을 보면 lr의 분모가 생겼음을 알수 있다. 해당 분모 값을 통해 비율을 조절하게 된다.분모에 있는 엡실론의 역할은 분모가 0이 되는걸 방지하기 위함이다. St를 보면 Gradient의 제곱을 해주는데 그 이유는 마이너스,플러스값이 나올수 있기 때문이다.

Gradient의 제곱은 언제나 양이기 때문에 계속 증가할 수밖에 없다. 그래서 lr 값이 아주 작게 설정되는 문제점을 안고 있다. 이를 해결한 것이 RMSprop이다.
* RMSprop

오래된 Gradient값에 가중치를 적용하여 영향력을 줄이도록 제한한다. 예를들어 위 분홍색 식에서 감마가 0.9라고 한다면 오래된 Gradient인 St-1에 0.9가 계속 곱해진다. 0.9*0.9*0.9*~~*0.9*오래된 Gradient +(1-0.9)*new Gradient.

* Adam(Adaptive Moment Estimation)

RMSProp와 거의 흡사하다. 차이점이 있다면 Momentum을 지수 가중 평균법으로 변경한 점이다. 또한 Adam은 베타1,베타2로 조절한다.
'Data Diary' 카테고리의 다른 글
| 2021-10-5(따릉이 프로젝트 완성하기 10) (0) | 2021.10.06 |
|---|---|
| 2021-10-04,05(딥러닝 CNN_기본 특징 설명) (0) | 2021.10.04 |
| 2021-09-26,29(딥러닝 CNN 1_활성화 함수의 이해 & 크로스 엔트로피) (0) | 2021.09.29 |
| 2021-09-28(따릉이 프로젝트 완성하기 9) (0) | 2021.09.28 |
| 2021-09-25(Learn github) (0) | 2021.09.25 |



