*본 내용은 시계열데이터 강의 내용 중 일부분을 요약한 내용입니다
오늘의 포스팅 내용은 다변량 선형확률입니다. 지금껏 진행 한 것은 Y가 1개인 경우였습니다. 다변량은 Y가 2개 이상인 것을 말합니다. 매출과 광고비가 있을때 단변량에서는 매출이 Y라고 정해놓고 시작했습니다. 하지만 반대로 광고비가 종속변수로써 영향을 더 많이 받는다면 말이 달라지게 됩니다. 따라서 어떤 변수가 가장 영향을 많이 받는 종속변수 인지를 알고자 할때 필요한게 단변량입니다.
단변량 알고리즘 중에서 대표적으로 벡터자기회귀 모형을 먼저 보겠습니다.
벡터자기회귀 모형(Vector Autoregressive Model)

교재에서는 위 내용을 VAR의 정의로 적혀 있는데 직관적으로 이해하기 힘들어서 구글링을 해봤습니다.
- 나의 과거에만 영향을 받는 모델: 자기회귀
- 나의 과거 뿐만 아니라 다른 변수의 과거에서도 영향을 받는 모델: 벡터자기회귀
다른 변수의 과거까지 수식으로 함께 넣다보니까 벡터 형식으로 표현이 가능합니다.
VAR(1)인 경우: 각 변수 한 타임 과거

Yt-1안에 A라는 변수 At-1과 B라는 변수 Bt-1이 함계 들어 있어서 이를 간단하게 표현한게 위 식입니다.
At-1,Bt-1 계수를 벡터형식으로 모아 놓은게 A1입니다. 참고로 꺽쇠가 있다는 것은 그 안에 여러개가 들어 있다는 뜻입니다.
실습: VAR 데이터생성 및 이해
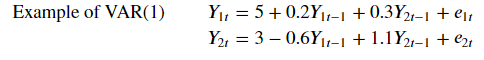
Y1t, Y2t를 묶어서 표현 한것이 Y[t]입니다. A1 벡터의 구성요소는 0.2, 0.3, -0.6, 1.1 입니다.
적용하는 방법은 실습을 통해 확인해 봅니다.
import numpy as np
import matplotlib.pyplot as plt
import statsmodels
import statsmodels.api as sm
#차수 입력
intercept = np.array([5,3])
matrix_A = np.array([[0.2,0.3], [-0.6,1.1]])
residual_covarinace = np.array([[1,0.8], [0.8, 2]])
# VAR 데이터 생성
fit = statsmodels.tsa.vector_ar.var_model.VARProcess(matrix_A, intercept, residual_covariance)
#시뮬레이션 시각화1
simul_num = 100
fit.plotsim(steps=sumul_sum, sseed=123) #100개 만큼 임의로 생성 후 시각화
plt.tight_layout()
plt.show() #첫번째, 두번째 그래프
# 시뮬레이션 시각화2_fit의 계수를 기반으로 시뮬레이션
# 임의로 데이터 두개를 시각화한 사실이 중요하다
# 예를들어 하나는 한국주식시장, 다른 하나는 미국 주식시장
simul_num =100
#sigma_u = corr과 같음
simul_values = statsmodels.tsa.vector_ar.util.varsim(fit.coefs, fit.intercept, fit.sigma_u, steps=simul_num)
plt.figure(figsize=(10,5))
plt.plot(simul_values)
plt.tight_layout()
plt.show() #두개가 겹친 그래프
#ACF 시각화
fit.plot_acorr()
plt.tight_layout()
plt.show()
'''
대각: Y1(1,1)에 대한 자기상관, Y2(2,2)에 대한 자기상관 (둘다 자기상관이 있음)
반 대각: Y1,Y2 서로에 대한 corr
'''
#VAR 모형적합
fit = sm.tsa.VAR(simul_values).fit()
display(fit.summary())
# 예측 및 시각화
# endog: 각 시점 마다의 계수가 출력된다
forecast_num = 20
pred_var =fit.forecast(fit.model.endog[-1;], steps = forecast_num)
pred_var_ci = fit.forecast_interval(fit.model.endog[-1:], steps=forecast_num)
fit.plot_forecast(forecast_num)
plt.tight_layout()
plt.show()
#잔차진단
fit.plot_acorr()
plt.tight_layout()
plt.show()
'''
각각의 autocorr이 작기때문에 화이트노이즈에 가깝다는 추론 할수있다.
'''


Results for equation이 y1과 y2 두개가 있습니다. y1을 한국시장, y2를 미국 시장이라고 했을때 방정식이 두개로 나뉘어서 어떤 변수가 종속변수로써 더 적합한지를 분석하게 됩니다. (equation=방정식)
한국시장은 0.085의 유의하지 않는게 하나 발견이 되었고 미국시장은 모두 유의하다고 나왔습니다. 따라서 미국시장이 다른 변수에 의해 많은 영향을 받고 있기 때문에 한국시장보다 미국시장이 종속변수로써 더 적합하다고 할수 있습니다.
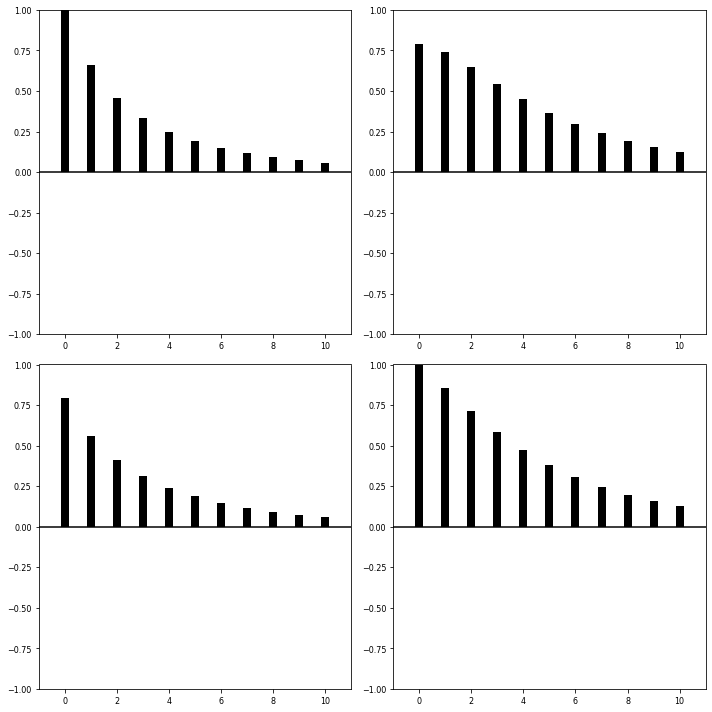
실선+도트는 신뢰구간이고 실선만 있는 것은 점추정 값입니다. 마지막 값이후로 steps 만큼 예측을 하게 됩니다.

임펄스 응답 함수(Impulse Response Function)
VAR 모형은 여러개의 시계열 상호상관관계를 기반으로 각각의 변수가 다른 변수에 어떤 영향을 주는지 임펄스 반응 함수로 알 수 있습니다. 즉 위 실습에서 y1은 한국주식시장, y2는 미국주식시장 이라는 가정에서 y1이 변화를 했을때 y2에 미치는 영향을 표시한 것입니다. 실습코드는 위 실습 내용과 이어짐을 알려 드립니다
# 임펄스반응함수 추정
#irf: impulse responsible function
#20라는 건 20lag을 뜻함
fit.irf(forecast_num).plot()
plt.tight_layout()
plt.show()
y1이 변화할때 y2에 끼치는 영향은 마이너스를 보이고 반대로 y2가 변했을때 y1에 끼치는 영향은 플러스입니다.
만일 주식시장아니라 소비(y1), 매출(y2)라고 했을때 소비가 줄면 매출도 감소하는 효과가 있다 라고 해석할수 있습니다.
실습2: 거시경제 VAR 모형화 및 해석
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels
import statsmodels.api as sm
#데이터 로딩
raw = sm.datasets.macrodata.load_pandas().data
dates_info =raw[['year','quarter']].astype(int).astype(str)
raw.index = pd.DateTimeIndex(sm.tsa.datatools.dates_from_str(dates_info['year']+'Q'+date_info['quarter']))
raw_use = raw.iloc[:,2:5]
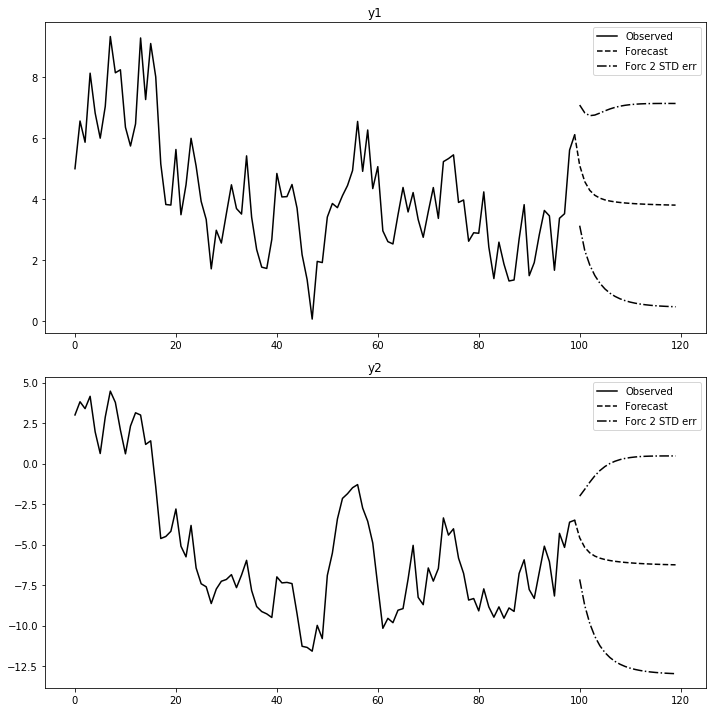
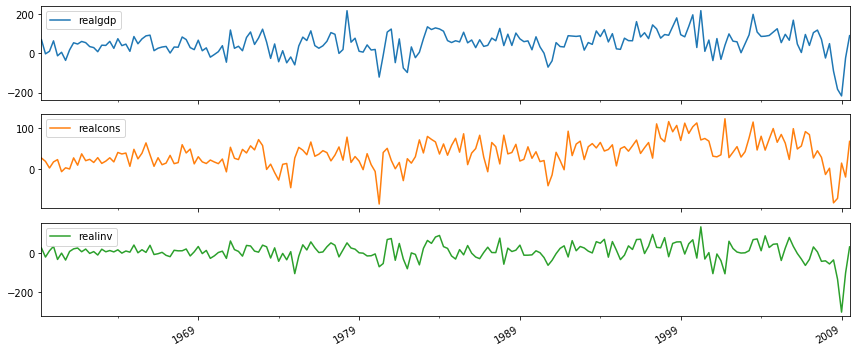
#데이터 시각화
raw_use.plot(subplots=True, figsize(12,5))
plt.tught_layout()
plt.show()
raw_use.diff(1).dropna().plot(subplots=True, figsize(12,5))
plt.tight_layout()
plt.show()
# VAR 모형적합
#추세를 제거한게 정상화가 될 확률이 높기때문에 이걸로 VAR모형적합을 한다
raw_use_return = raw_use.diff(1).dropna()
fit = sm.tsa.VAR(raw_use_return).fit(maxlags=2) #p=2
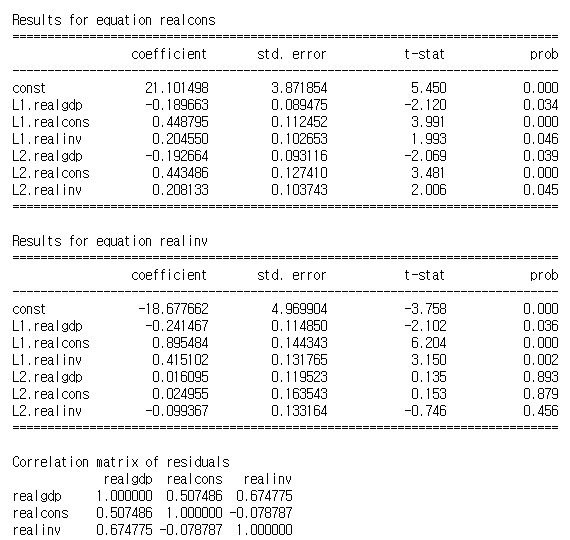
display(fit.summary())
'''
realcons(소비)이 가장 유의한 변수가 많다. 6가지 변수가 realcons에 영향을 준다는 뜻이며
가장 종속성이 짙은걸 알수있다.
'''
#예측 및 시각화
forecast = 20
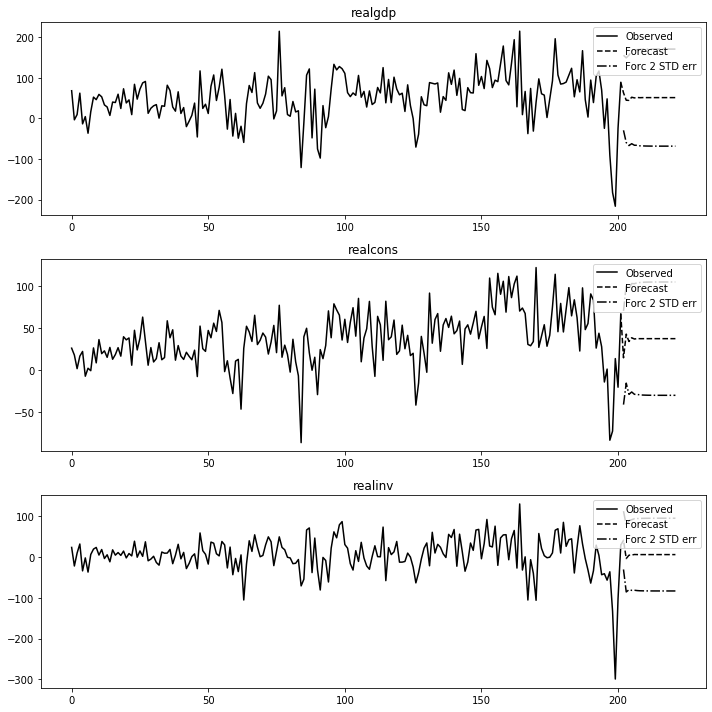
fit.plot_forecast(forecast_num)
plt.tight_layout()
plt.show()
#임펄스반응함수 추정
fit.irf(forecast_num).plot()
plt.tight_layout()
plt.show()
# 잔차진단
fit.plot_acorr()
plt.tight_layout()
plt.show()
'''
튀는 값이 있긴하지만 전반적으로 WN에 가깝다는 것만 알고 넘어간다다
'''


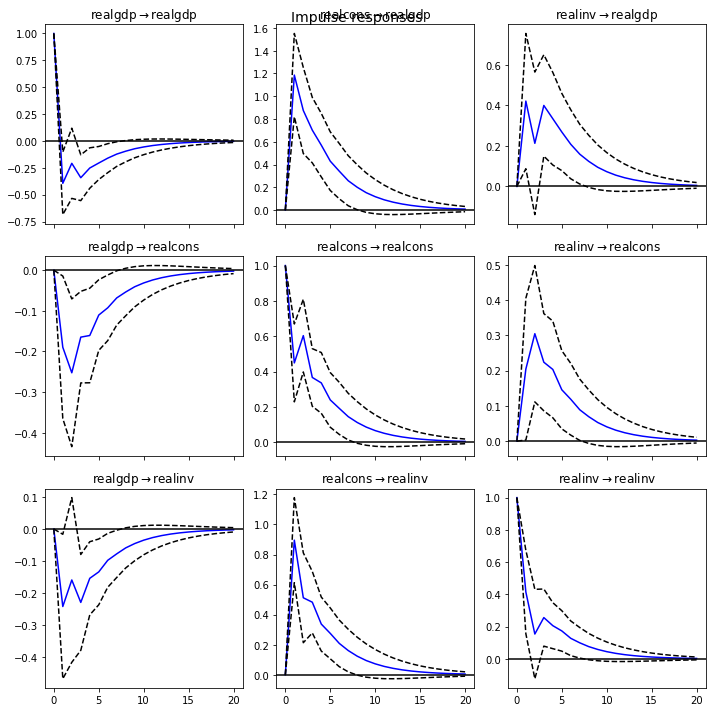
1.realcons, realinv는 특정 시차동안 꾸준하게 양수의 효과를 보인다.
2.realgdp->realcons: gdp가 1만큼증가시 realcons가 오히려 감소한다. 즉 gdp가 증가한다고 해서 바로 소비로 이어지지 않는다 오히려 줄인다
3. realinv->realcons: 투자가 늘면 소비도 증가한다.
4.realcons -> realgdp: 소비를 늘리면 gdp가 1이상 늘어나는 긍정적인 효과를 보인다.
그래서 gdp를 늘리려면 realinv를 늘리는 것 보다는 소비를 늘리는게 효과가 좋다

각각의 autocorr이 작기때문에 화이트노이즈에 가깝다는 추론 할수있다.
그래인저 인과관계 모형(Granger Causality Model)
Spurious Regression: X와 Y가 관련(인과관계)이 없거나 논리적인 스토리가 없음에도 단순하게 상관성이 높다라는 공격
X,Y 둘간의 관련성이 없는데 단순히 상관성 있다는 것이 마치 인과성이 있다고 해석하는게 Spurious(거짓된, 겉으로만 그럴싸한) Regression 용어이다.
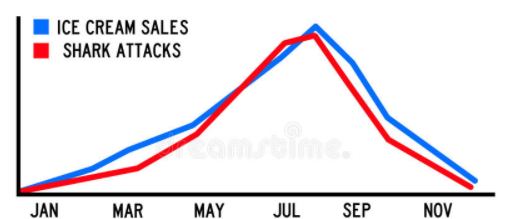
그래프상에서 아이스크림과 상어공격이 언뜻 상관성이 있어보인다. 아이스크림 매출 증가시 상어 공격 건수도 증가하므로 이 둘은 인과관계가 있다고 착각하는게 Spurious Regression이다.
단지 여름이라서 아이스크림 판매와 상어 공격이 많아진것이 올바른 인과관계이다.
이를 더 확장해서 생각해 보면 실생화의 징크스도 해당이 된다.
- 징크스: 머리를 염색했더니 시험점수가 100점이 나오더라
머리염색을 한 후에 시험을 치뤘더니 100점이 나왔다는 징크스얘기는 머리염색이 원인이라는 인과관계 형태를 보인다.
머리염색과 시험성적의 인과관계를 우리는 규명할수가 없다. 하지만 정말로 머리염색을 한 후 (선행) 의 시험성적은 영향을 받는지에 대한 인과관계는 확인해 볼수 있다. 다시 말하면 인과관계는 파악 못하지만 시간 흐름에 따른 인과관계를 파악하고자 할때를 Granger Causality라는 개념을 사용해서 확인할수 있다. 아래 예를들어본다.
- 추론불가한 문제: "닭이 먼저인가 달걀이 먼저인가?" (인과관계)
- 추론가능한 문제: "닭과 달걀의 생성순서 별 서로의 영향력은 어떤가?" (Granger 인과관계)
Granger Causality를 사용하기 위한 조건들이 있다.

just use Y식을 보면 X(다른 변수)가 없고 오직 자기자신의 과거만 해당이 된다. 현재는 과거의 나에게 얼만큼 영향을 주는지를 알수있고
use X and Y에서 베타X 가 있는데 위 이미지처럼 Y가 달걀 X가 닭이라고 했을때 달걀의 생산량은 닭의 생상량에 얼마큼 영향을 받고 있는지를 알수가 있다.
이해를 돕기위해서 아래 실습을 실행한다.
실습: 닭과 달걀의 생산량을 통한 Granger 인과관계 이해
# 닭과 달걀을 시간적 순서로 봤을때 어떤게 선행성이 있는가
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
#데이터 로딩
location = './Data/ChickenEggProduction/Chicken_Egg_Production.txt'
raw_all = pd.read_csv(location, sep='\t')
raw_all.head()
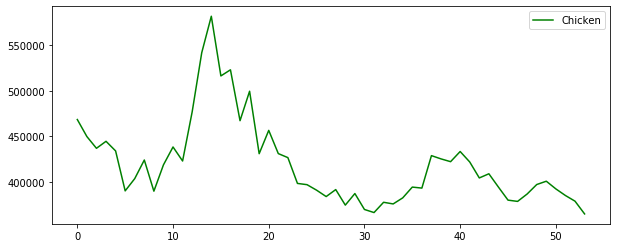
#데이터 시각화
plt.figure(figsize=(10,4))
plt.plot(raw_all['Chicken'], 'g', label='Chicken')
plt.legend()
plt.show()
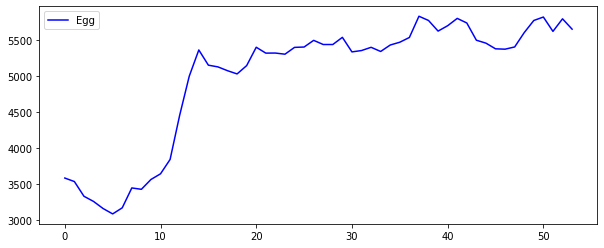
plt.figure(figsize=(10,4))
plt.plot(raw_all['Egg'], 'b', label='Egg')
plt.legend()
plt.show()
# 정상성 변환시각화
# 정상성을 가져야 실행이 되므로 diff를 적용
plt.figure(figsize=(10,4))
plt.plot(raw_all['Chicken'].diff(1), 'g', label='Diff(Chicken)')
plt.legend()
plt.show()
plt.figure(figsize=(10,4))
plt.plot(raw_all['Egg'].diff(1),'b',label='Diff(Egg)')
plt.legend()
plt.show()
# Granger Causality 테스트
print('\n[Egg -> Chicken]')
#maxlag 몇개의 파라미터를 적용할것이가(lag값)
#addcons 상수항 적용 여부
#맨 처음 x의 입력은 array 형식이여야 하므로 values
'''
알고리즘 설계상 두번째 컬럼이 첫번째 컬럼에 영향을 주는지를 분석하므로 달걀이 두번째 컬럼으로 와야한다.
iloc[:,1:] -> 컬럼이 닭,달걀순이므로 두번째 컬럼인 달걀이 닭에 Granger Causality가 있는지를 본다
'''
granger_result1 = sm.tsa.stattools.grangercausalitytests(raw_all.diff(1).dropna().iloc[:,1:].values, maxlag=3, verbose=True)
'''
lag1~3 통계량을 봤을때 p-value가 5%보다 작으므로 X가 Y에 영향을 준다
'''
print('\n[Chicken -> Egg]')
#순서 바꾸기 닭->달걀
granger_result2= sm.tsa.stattools.grangercausalitytests(raw_all.diff(1).iloc[:,[2,1]].values, maxlag=3, verbose=True)
'''
전혀 도움이 되고 있지 않다.
즉, 달걀->닭이다.
'''
# 의사결정
# 닭이 달걀을 낳으면 그 수는 약 3년후까지 닭의 수에 영향을 준다
# 왜 3년? lag3까지 유의하게 나왔기 때문
# 닭의 수가 많아진다고해서 달걀을 많이 낳지는 않는다
# 달걀 -> 닭 (Granger Causality) 달걀이 닭에 Granger Causality 경향을 보인다.



달걀->닭 인 경우 lag3까지 모두 유의하며, 닭-> 달걀 인 경우 lag1까지만 유의하다
(좀더 자세한 설명은 코드 맨 밑에 있습니다)
'Data Diary' 카테고리의 다른 글
| 2021-04-08기록 (0) | 2021.04.08 |
|---|---|
| 2021-04-07(시계열데이터 심화14_공적분 모형) (0) | 2021.04.07 |
| 2021-04-05(시계열데이터 심화12_arima 자동화&prophet) (0) | 2021.04.05 |
| 2021-04-03 기록 (0) | 2021.04.03 |
| 2021-04-02 기록(1차 방문) (0) | 2021.04.03 |

