*본 내용은 시계열데이터 강의 내용 중 일부분을 요약한 내용입니다
전 포스팅까지는 선형알고리즘을 다뤘다면 오늘 포스팅은 비선형 알고리즘에 대한 간략한 개념정도만
올리겠습니다. 비선형이 상당히 많은 내용과 복잡한 내용이 있다고 하셔서 깊은 내용까지는 강의에서 다루지 않았어요
확실히 선형보다는 복잡한 수식이 많았습니다. 저도 완전히 100% 숙지 한게 아니라서 부족한 설명이 있더라도
양해 부탁드리겠습니다
상태 공간 모형(State Space Models)

상태 공간 모형에 앞서서 위 이미지를 통해서 비선형이 뭔지를 먼저 설명드리겠습니다.
지구의 온도를 측정하기 위해서 태평양 온도 수치를 녹색이라 하겠습니다. 파란색도 태평양 온도이긴 하지만
실제로 측정한 값이 아니고 다른 우회적인 방법을 통해서 얻어낸 근사값이라고 가정 합니다.
이때 Y는 지구의 온도, X를 근사값으로 얻어낸 파란색이라고 설정하겠습니다.
여기서 우리는 이 X가 정말 태평양 온도를 잘 대변하고 있는지를 의심해봐야 합니다. 위 예에서는 실제값과 근사값을 나눠서 설명드렸지만 실제에서는 근사값인지 실제값인지, 근사값이 실제값과 같은지 등 아무 정보가 없습니다.
여지껏 올린 포스팅에서는 X에 대해서 어떠한 의심없이 바로 X로 적용 시켰습니다.
비선형은 '의심' 이라는 관점에서 출발 합니다. 이 X를 그냥 넘기지 말고 정확한 값으로 '추정' 해보겠다는 것입니다.
따라서 X는 정확한 데이터가 아니니까 이를 별도로 추정해 보는 행위가 비선형의 목적입니다.
기존 방정식은 Y=f(x)+잡음 입니다. 이 X를 녹색값이 되도록 추정할려면 아래와 같은 식이 있어야 합니다.
X= g(x')+잡음
상태 전이식이 X를 추정하기 위한 부분입니다. 상태변수 라는 것은 이 X처럼 추정하는 것들을 일컫는 말입니다.

위 사실을 통해 알수 있는 점은 X를 추정할수 있다는 개념이고 이 변수 이름을 상태변수라고 일컫는 것입니다.
지수평활법(Simple Exponential Smoothing)

정리하면 추세나 계절성 패턴이 없는 데이터를 예측할때 사용가능합니다.
왜일까요? 생각을 해봤는데 이유를 아래 식과 같이 설명해보겠습니다.

제 나름 이유를 말씀드리자면 1번 식 or 2번 식 모두 아주 먼 과거 데이터에도 똑같은 가중치를 매긴다는 점에서
추세와 계절성이 성립이 안되는 게 아닐까 합니다.
추세라면 증감의 경향을 나타내는데 이는 현재 데이터와 과거로 갈수록 데이터간의 차이가 나게됩니다.
예를 들어 증가하는 경향의 데이터라면 현 시점의 데이터는 값이 100이고 맨 처음 데이터 값은 5라고 했을때 차이가 많이 납니다. 다음 시점을 예측하기 위해서 5가 나온 시점과 100이 나온 시점을 같은 가중치로 계산하겠다는 것입니다.
상식적으로 납득이 안됩니다. 가장 최근 데이터 일수록 가중치를 높게 주는게 경향 파악에 유리 할 것입니다.
그래서 위 식을 이용할 경우에는 아무 패턴이 없는 데이터에만 효과가 있는게 아닌가 생각합니다.
선형 추세 알고리즘 by Holt

추세패턴이 잡을때 사용하는 예측알고리즘입니다. 추세패턴이라면 ARIMA를 생각나게 하는데요
이 알고리즘은 Level이라는 상태변수와 b라는 상태변수로 구성되여 있습니다. 상태변수니까 각각을 구성하는 방정식이 존재합니다. 추정한다는 것입니다.
여기에서 는 시간 t에서 시계열의 수준 추정 값, 는 시간 에서의 시계열의 추세(기울기) 추정 값, 0≤α≤1은 수준에 대한 매개변수, 0≤β∗≤1은 추세에 대한 매개변수를 나타냅니다.
강의에서 훑고 지나가는 정도라서 자세한 원리는 잘 모르겠지만 일단 여기서 알고 넘어 가야 하는건 추세를 반영한 상태 변수가 있다는 것 정도입니다.
추세알고리즘이 있다면 당연히 계절성 알고리즘도 있습니다.
계절 알고리즘 by Holt-Winter
선형 추세 알고리즘에 계절성을 반영한 예측 알고리즘입니다. 위에서 본 추세 알고리즘에서 계절성이 추가됩니다.
시계열 데이터는 분해가 가능한데 이때 덧셈으로 분해가 되는지 곱셈으로 분해가 되는지에 따라 addive, Multiplicative 로 구별되였습니다. 이와 마찬가지로 각 경우에 따라 분해 방식이 조금씩 달라지는데 자세한 것은 아래를 참고해주세요

로컬레벨 모형(Local Level Model)
랜덤워크 모형에 관측잡음이 추가된 것으로 랜덤워크 과정을 따르는 단변수 상태변수 𝜇𝑡μt를 가집니다.
맨 위에서 지구온도를 Y, 태평양 온도를 X라고 정했는데 여기서 X가 램덤워크 일 경우입니다.
따라서 Xt= Xt-1+잡음이 되고 Yt=Xt+ 잡음이 됩니다. 랜덤워크는 비 정상성이므로 차분을 해줘야하는데
이는 위에서 설명한 것처럼 ARIMA를 연상케 합니다.

그러면 이 둘의 차이점은 뭘까?


예시를 보면 배를 찾기 위해서 바다의 진동에 의해 이동된 잡음을 이용해서 거리를 구할때 로컬 레벨 모형에 해당됨을 이해할수가 있습니다.
실습: 로컬레벨 모형 데이터생성 및 이해
# 데이터 생성
np.random.seed(123)
model_generator = KalmanFilter(k_endog=1, k_states=1,
transition=[[1]], selection=[[1]], state_cov=[[10]],
design=[[1]], obs_cov=[[1]])
y_gener, x_gener = model_generator.simulate(100)
# 데이터 생성
plt.figure(figsize=(10,6))
plt.plot(y_gener, 'r:', label="Observation Values")
plt.plot(x_gener, 'g-', label="State Values")
plt.legend()
plt.title("Simulation of Local Level Model ($\sigma_w^2 = 10$, $\sigma_v^2 = 1$)")
plt.show()
# 데이터 생성
np.random.seed(123)
model_generator = KalmanFilter(k_endog=1, k_states=1,
transition=[[1]], selection=[[1]], state_cov=[[1]],
design=[[1]], obs_cov=[[10]])
y_gener_target, x_gener_target = model_generator.simulate(100)
# 데이터 생성
plt.figure(figsize=(10,6))
plt.plot(y_gener_target, 'r:', label="Observation Values")
plt.plot(x_gener_target, 'g-', label="State Values")
plt.legend()
plt.title("Simulation of Local Level Model ($\sigma_w^2 = 10$, $\sigma_v^2 = 1$)")
plt.show()
# 로컬레벨모형 추정
fit = sm.tsa.UnobservedComponents(y_gener_target, level='local level').fit()
fit.summary()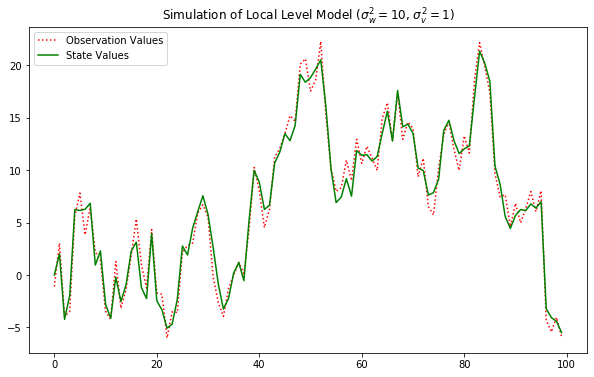

이 둘의 그래프 모양이 다릅니다. state values 는 랜덤워크에 해당되는 값입니다. 빨간 실선은 실제값입니다.
실제값에서 랜덤워크가 차지하는 비중을 볼수 있습니다.
왼쪽의 녹색은 실제값과 거의 유사합니다. 즉 랜덤워크의 비중이 크다는 걸 알수 있습니다(state_cov=10)
반대로 오른쪽은 랜덤워크가 차지 하는 비중이 작습니다. Yt= Xt+ 잡음 에서 잡음의 크기가 크고 Xt는 작다는 얘기입니다.
상태공간모형 기반의 시계열 "구조화모형"

여러개의 보이지않은 성분들로 분리하는 것이 구조화모형의 특성입니다.
아래 실습은 주기특성과 AR 특성을 각각 추출하는 내용입니다. 사이클 먼저 보도록 하겠습니다
# 구조화모형 추정
# rwalk: 랜덤워크
# damped_cycle: 안정적으로 사이클을 추정
model = sm.tsa.UnobservedComponents(unemployment_US, level='rwalk', cycle=True,
stochastic_cycle=True, damped_cycle=True)
result = model.fit(method='powell')
display(result.summary())
'''
unemployment_US를 랜덤워크와 stochastic_cycle로 분해한다
'''
# 추정 시각화
fig, axes = plt.subplots(2, figsize=(10, 6))
axes[0].plot(unemployment_US.index, unemployment_US.UNRATE,
label='Unemployment Rate')
# result.level.smoothed 추정된 값
axes[0].plot(unemployment_US.index, result.level.smoothed, label='Random Walk')
axes[0].legend(loc='upper left')
axes[0].set(title='Level/Trend Component')
axes[1].set(title='Cycle Component')
axes[1].plot(unemployment_US.index, result.cycle.smoothed, label='Cyclic')
axes[1].legend(loc='upper left')
fig.tight_layout()
plt.show()
# 잔차진단
result.plot_diagnostics(figsize=(10, 8))
plt.show()
데이터에서 싸이클 패턴만 뽑힌 시각화입니다. 밑에 있는 AR 시각화 비교하면 상당히 비슷한 모양입니다.
# 구조화모형 추정
model = sm.tsa.UnobservedComponents(unemployment_US, level='rwalk', autoregressive=4)
result = model.fit(method='powell')
display(result.summary())
# 추정 시각화
fig, axes = plt.subplots(2, figsize=(10,6))
axes[0].plot(unemployment_US.index, unemployment_US.UNRATE, label='Unemployment Rate')
axes[0].plot(unemployment_US.index, result.level.smoothed, label='Random Walk')
axes[0].legend(loc='upper left')
axes[0].set(title='Level/Trend Component')
axes[1].set(title='AR Component')
axes[1].plot(unemployment_US.index, result.autoregressive.smoothed, label='AR')
axes[1].legend(loc='upper left')
fig.tight_layout()
plt.show()
# 잔차진단
result.plot_diagnostics(figsize=(10,8))
plt.show()
확률적 변동성 모형 (Stochastic Volatility Model)

식이 복잡해지고 고차원으로 들어가면 잔차는 SARIMAX를 시용해도 WN이 되지 않습니다.
이때 이 잔차를 변동성이라고 부르고 이를 상태변수로 취급을해서 g(잔차)로 변동성을 추정한다는 개념
따라서 변동성 패턴을 잡기 위한 모형입니다.
'Data Diary' 카테고리의 다른 글
| 2021-04-12(시계열데이터 심화16_딥러닝) (0) | 2021.04.12 |
|---|---|
| 2021-04-10 기록(시계열 데이터 심화_비선형 복습) (0) | 2021.04.10 |
| 2021-04-08기록 (0) | 2021.04.08 |
| 2021-04-07(시계열데이터 심화14_공적분 모형) (0) | 2021.04.07 |
| 2021-04-06(시계열데이터 심화13_VAR&Granger Causality ) (0) | 2021.04.06 |

