H_record

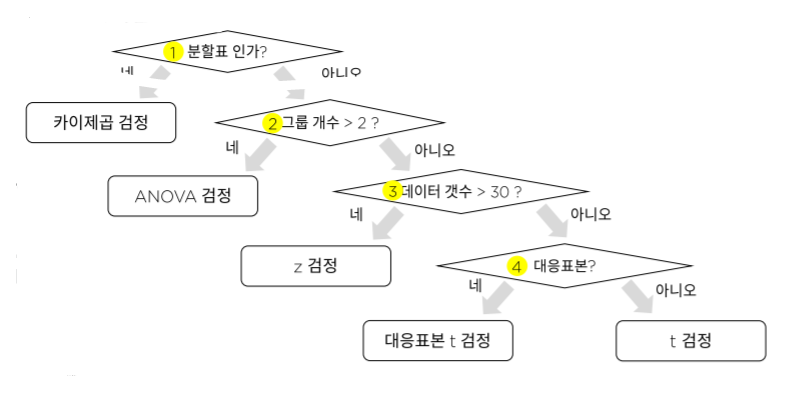
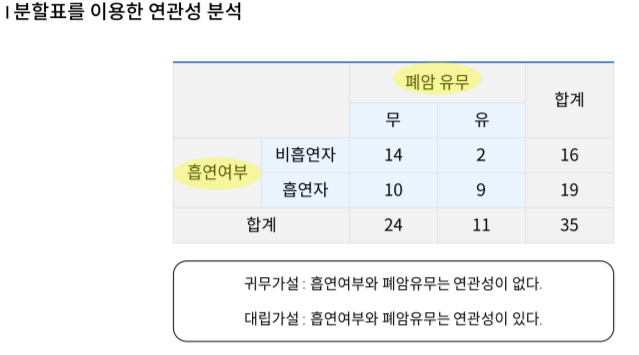
빨간색 부분이 오늘 진행한 내용입니다.

태양열 프로젝트

1차 시도. 랜덤 포레스트 log 상태에서 스케일링에 따른 변화
-> 변화 없음

2차 시도. log 아닌 상태에서 스케일링에 따른 변화
->Normalizer

3차 시도. 변수의 차분 변화에 따른 성능 측정
->변수 2개 이상 동시 사용 시 성능 저하 발생

4차 시도. extracted_features 활용
-> 모든 변수 사용시 성능 저하 발생하여 VIF 및 RFECV 실행

 extracted_features 함수를 통해 얻은 변수들 중 의미 있어 보이는 120여 개 피처들로 예측한 그래프입니다.

성능값이 23점을 기록했습니다;;

120여개의 피처들을 vif를 통해 추리고, 추린 값을 refecv를 통해 또 추려봤습니다. 120개의 피처를 refecv를 돌리면 에러가 발생해서 vif 통해 1차적으로 걸렀습니다. 그래서 vif을 통해 얻은 피처 VS vif+refecv을 통해 얻은 피처들을 각각 랜덤 포레스트에 돌렸고 결과는 아래와 같습니다. 기존 변수 활용 시 성능은 7.801이었습니다.

* VIF : 7.98 (성능다운)
* refecv: 7.98(성능다운)

ㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎㅎ

5차 시도. 랜덤 포레스트 그리드 서치

-> 랜덤포레스트 그리드 서치를 실행했습니다. 
{'criterion': 'mse',
 'max_depth': None,
 'max_features': 'auto',
 'min_samples_leaf': 2,
 'min_samples_split': 8,
 'n_estimators': 300}

앞서 구한 결과를 토대로 적용한 결과
* 7.96 (성능다운)

6차 시도. 계절성 분해 적용

-> target값을 분해한 후 validation data인 2021년 01월 추세&계절 값은 2020년도 01월 값을 사용했습니다.
랜덤 포레스트: 13.98 (추세+계절)
랜덤포레스트: 7.78(계절), 약 0.02 개선

7차 시도. Cloud lag값 제거

-> 7.73으로 성능 개선됨

8차 시도. ['Temperature','WindSpeed','Humidity'] 차분 횟수에 따른 성능변화

-> 차분 6일 때 가장 좋은 성능을 보임

1. diff -> 3 : 7.580
2. diff -> 4 : 7.510
3. diff -> 5 : 7.599
4. diff -> 6 : 7.435
5. diff -> 7 : 7.589 (차분 7회 이상부터 과적합)
6. diff -> 8 : 7.645
7. diff -> 9 : 7.702
8. diff -> 10 : 7.753

9차 시도. 랜덤 포레스트 estimator 변경에 따른 성능변화

300 : 7.369
400: 7.363
500: 7.326
600: 7.314
700: 7.331
800: 7.350
900: 7.340
1000: 7.360

10차 시도. 수정된 피처를 적용한 그리드 재검토

*그리드 결과

'max_depth': None, 
'min_samples_leaf': 6, 
'min_samples_split': 14, 
'n_estimators': 600

-> 정확도 83%, Score : 7.51
기존 7.31 보다 0.2 낮아짐. min_samples_leaf & min_samples_split는 과적합 방지로 사용한다. 기존에 사용하던 값은 디폴트 값을 이용했으므로 과적합에 취약한 모델일 가능성이 있다. 하지만 validation 값은 앞서 언급했듯이 0.2가 낮아진 상태이다. 어떤 파라미터가 옳은지는 사실 잘 모르겠다. 일단 val값을 가장 낮추는 방향으로 진행할 예정이다.

11차 시도. Cloud의 더미 변수화

-> 7.526으로 개선 효과 없음

12차 시도. day 데이터의 lag 적용

day lag값 -> 24,48 인 경우 7.249 성능개선
day lag값 -> 24,48,72 인 경우 7.26 성능감소 
day lag값 -> 24,48,72,96 인 경우 7.35 성능감소 

R

*Decision tree

위와 같은 데이터가 있을때 의사결정나무를 사용한다면 아래와 같은 모양으로 나타낼수 있다.

각 피처들을 노드로 사용하여 분류에 분류를 거듭한다. 가장 처음에 나온 노드인 날씨테스트는 어떤 기준으로 선정 된것인가? 엔트로피를 사용하여 노드의 순서를 정할수 있다.  

각 노드 별 무질서를 구할때 엔트ㅗ피를 사용하는데, 무질서는 양성,음성이 뒤섞여 있는 있을때 높은 수치를 보인다. 

날씨는 맑을때 배드민턴을 친다는 사람이 4명이면 무질서는 0(난잡하지 않다), 반면 친다는 사람 2명, 아닌 사람 2명씩 있으면 막 뒤섞여 있으므로 무질서하다. 특히 이처럼 5:5 비율일 경우에는 무질서가 가장 높게 측정 된다. 한쪽으로 치우칠수록 분류가 잘되는 방향이기 때문이다. 

값이 1/2 일때 가장 높은 무질서 값 1을 기록한다. 엔트로피 활용은 아래 그림처럼 사용된다.

날씨 테스트의 전체 무질서 값은 얼마인지 계산하여 각 노드에 들어올 순서를 정해 줄수 있다.

이로써 각 노드의 무질서값을 알수있다. 첫번재 노드는 날씨테스트를 시작으로 바람 -> 온도 -> 습도 순으로 분류가 진행될것이다. 

의사결정나무의 단점은 과적합이다. 다시 말하면 일반화 하기엔 문제가 있다는 것이다. 왜?? 위와 같은 트리는 노드들의 순서가 정해져 있다. 이렇게 되면 일반화하기엔 무리가 있다. 이를 보완 위해서 랜덤포레스트를 사용한다. 

install.packages('tree')
library(tree)
library(caret)

rawdata <- read.csv(file='wine.csv', header=TRUE)
rawdata$Class <- as.factor(rawdata$Class)
str(rawdata) #데이터 형태를 볼수 있다.

analdata <- rawdata
set.seed(2021)
datatotal <- sort(sample(nrow(analdata),nrow(analdata)*.7))
train <- rawdata[datatoal,]
test <- rawdata[-datatoal,]
str(train)
str(test)

#모델
library(tree)

#기본트리 
treeRaw <-  tree(Class~., data=train)
plot(treeRaw)
text(treeRaw) #Cv,가지치기 하지 않은 가장 기본적인 트리

#기본트리-> 가지치기위해서 적절한 사이즈(depth) 찾기
#prune.misclass: 오분류 기준
cv_tree <- cv.tree(treeRaw, FUN=prune.misclass)
plot(cv_tree)
#사이즈를 바꿔가며 오분류율을 본다. 최적의 사이즈:3
#사이즈가 높다 -> 트리가 많다 -> 피처들을 많이 사용해야한다 -> 복잡도가 올라간다
#너무 단순해도, 너무 복잡해도 안된다.

#사이즈 4로 가지치기(pruning)
prune_tree <- prune.misclass(treeRaw, best=4)
plot(prune_tree)
text(prune_tree,pretty = 0)

#예측하기
pred <- predict(prune_tree, test, type='class')
confusionMatrix(pred,test$Class)
#의사결정은 과적합 가능성이 높다 

*랜덤포레스트

쉽게 생각하면 위와 같은 트리구조를 여러개 만든다. 피처들의 순서가 고정된 것이 아니라 여러가지의 경우의 수를 만들어 가면서 트리를 많이 만들어서 일반화에 가깝게 만든다.

주어진 데이터의 행을 추출하는데 중복이 가능하다. 2단계는 피처를 임의의 d개 만큼 뽑아서 의사결정나무처럼 트리구조를 만들어서 분류한다. 여러 트리를 만든 후에는 다수결 원칙?에 따라 최종 결과가 정해진다.

library(caret)
rawdata <- read.csv(file='wine.csv', header=TRUE)
rawdata$Class <- as.factor(rawdata$Class)
str(rawdata) #데이터 형태를 볼수 있다.

analdata <- rawdata
set.seed(2021)
datatotal <- sort(sample(nrow(analdata),nrow(analdata)*.7))
train <- rawdata[datatoal,]
test <- rawdata[-datatoal,]
str(train)
str(test)

#모델
ctrl <- trainControl(method='repeatedcv',repeats=5)
rfFit <- train(Class~.,
               data=train,
               method='rf',
               trControl=ctrl,
               preProcess=c('center','scale'),
               metric='Accuracy')
rfFit
plot(rfFit)
#mtry: 랜덤 피처 갯수가 2일때 가장 좋다

#예측
pred_test <- predict(rfFit,newdata=test)
confusionMatrix(pred_test,test$Class)

#변수 중요도
importance_rf <-  varImp(rfFit, scale=FALSE)
plot(importance_rf)

태양열 프로젝트

첫번째 시도. 랜덤 포레스트 log 상태에서 스케일링에 따른 변화
-> 변화 없음

두번째 시도. log 아닌 상태에서 스케일링에 따른 변화
->Normalizer

세번째 시도. 변수의 차분 변화에 따른 성능 측정
->변수2개이상 동시 사용시 성능 저하 발생

네번째 시도. extracted_features 활용
-> 모든 변수 사용시 성능 저하 발생하여 VIF 및 RFECV 실행

 extracted_features 함수를 통해 얻은 변수들중 의미있어 보이는 120여개 피처들로 예측한 그래프입니다.

성능값이 23점을 기록했습니다;;

120여개의 피처들을 vif를 통해 추리고, 추린 값을 refecv를 통해 또 추려봤습니다. 120개의 피처을 refecv를 돌리면 에러가 발생해서 vif통해 1차적으로 걸렀습니다. 그래서 vif을 통해 얻은 피처 VS vif+refecv을 통해 얻은 피처들을 각각 랜덤포레스트에 돌렸고 결과는 아래와 같습니다. 기존 변수 활용시 성능은 7.801이였습니다.

* VIF : 7.98 (성능다운)
* refecv: 7.98(성능다운)

다섯번째 시도. 랜덤포레스트 그리드 서치

-> 랜덤포레스트 그리드 서치를 실행했습니다. 
{'criterion': 'mse',
 'max_depth': None,
 'max_features': 'auto',
 'min_samples_leaf': 2,
 'min_samples_split': 8,
 'n_estimators': 300}

앞서 구한 결과를 토대로 적용한 결과
* 7.96 (성능다운)

여섯번째 시도. 계절성 분해 적용

-> target값을 분해한 후 validation data인 2021년 01월달 추세&계절값은 2020년도 01월 값을 사용했습니다.
랜덤포레스트: 13.98 (추세+계절)
랜덤포레스트: 7.78(계절), 약 0.02 개선

개선된 값을 통해 SARIMAX에 적용 중입니다. 결과는 내일 포스팅 하겠습니다.

오늘은 R보다는 태양열 프로젝트를 주로 작업했습니다. 곧 있으면 마감인데 원하는 만큼 결과물이 좋지 않아서 조바심이 나네요. 먼저 R 요약 내용입니다.

R(나이브베이즈)

나이브베이즈 알기 전 조건부 확률 개념 먼저 보겠습니다.

축구 경기할 때의 승리/패배할 경우는 위와 같습니다. 이 중 승리를 하는데, 선제골의 여부에 따라 승리할 확률을 구할 수 있습니다. 종종 축구 경기 보면 캐스터가 말하길 "우리가 선제골을 넣으면 주로 승리를 하는데요 ~ " 혹은 '홈에서 경기를 하면 승리를 하는데요~' 이 모든 게 조건부 확률입니다. 식으로 나타내면 1번부터 3번까지 차례로 나타낼 수 있습니다.

2 번식을 1번에 대입하면 3번이 됩니다. 중요하게 볼 식은 3번입니다. 3번에 대해 자세히 살펴보겠습니다.

P(Y)가 조건이므로 P(x)는 당연히 아직 실행되지 않았습니다. 즉, 발생하기 전 확률이라 하여 사전 확률입니다. 이때 P(Y)은 

P(Y)는 상수이라고 하는데요 제 나름대로 예를 들자면..

동전 앞과 뒤, 둘 중 뭐가 나올지 모르기 때문에 둘 다 확률변수지만 앞이라는 조건이 결정이 되면 이는 확률변수가 아닌 상수로써 조건이 주어진 것이다. 즉 주어진 조건은 확률변수가 아닌 고정된 상수로 본다는 뜻이다.
P(X|Y) =  P(X) * P(Y|X) / P(Y) 에서 P(Y)는 고정된 값이므로 P(X|Y) 는 P(X) * P(Y|X) 값에 비례한다(이게 핵심)

*헷갈리지 않게 다시 정리
P(X|Y)의 조건 P(Y)는 상수이고, 그냥 단독적인 P(Y)는 확률변수이다.

조건으로 주어졌다는 것은 조건은 실행이 된다는 전제가 깔립니다. 시행이 되었으므로 어느 값을 가진 상수라는 것입니다. 상수는 한번 결정되면 변하지 않습니다. 따라서 분자인 P(X) * P(Y|X)에 따라서 비례를 한다 라는 것입니다.

R의 caret 패키지를 통해 구현하는 방법을 보겠습니다.

#데이터 불러오기
library(caret)
rawdata <- read.csv(file='heart.csv', header = TRUE)
str(rawdata)

#타켓 클래스 범주화
rawdata$target <- as.factor(rawdata$target)
unique(rawdata$target)

#연속형 독립변수의 표준화
rawdata$age <- scale(rawdata$age)
rawdata$trestbps <- scale(rawdata$trestbps)
rawdata$chol <- scale(rawdata$chol)
rawdata$thalach <- scale(rawdata$thalach)
rawdata$oldpeak <- scale(rawdata$oldpeak)
rawdata$slope <- scale(rawdata$slope)

#범주형 독립변수 
newdata <- rawdata
factorVar <- c('sex','cp','fbs','restecg','exang','ca','thal')
newdata[,factorVar] = lapply(newdata[,factorVar],factor)

#데이터 분리
set.seed(2020)
datatotal <-  sort(sample(nrow(newdata),size=nrow(newdata)*0.7))
train <- newdata[datatotal,]
test <-  newdata[-datatoal,]

train_x <- train[,1:12]
train_y <- train[,13]

test_x <- test[,1:12]
test_y <- test[,13]

#모델설정
ctrl <- trainControl(method='repeatedcv',repeats = 5)
nbFit <- train(target~.,
                  data=train,
                  method="naive_bayes",
                  trControl=ctrl,
                  #preProcess=c('center','scale'),
                  metric="Accuracy")
plot(nbFit)

#예측
pred_test <- predict(nbFit,newdata=test)
confusionMatrix(pred_test, test$target)

약 82%의 성능을 보였습니다. 스케일링을 하면 성능이 떨어져서 주석처리했습니다.

태양열 예측

첫 번째 시도:랜덤 포레스트 log 상태에서 스케일링에 따른 변화
-> 변화 없음

두 번째 시도: log 아닌 상태에서 스케일링에 따른 변화
->year 변수 삭제 후 MinMax or Robust 사용 시 가장 좋은 성능을 보임

세 번째 시도: 변수의 차분 변화에 따른 성능 측정(온도, 습도 등 차분을 통해 증감을 표현하여 패턴을 설명하고자, Cloud의 lag을 통해 1시간 전 Cloud가 끼치는 영향을 보고자)
->변수 2개 이상 동시 사용 시 성능 저하 발생, 가장 좋은 조합은.. 

랜덤포레스트'

'CV Score : '

7.801435294117648

'lgb'

'CV Score : '

8.27872655535256

많은 조합을 실험해 본 결과 위와 같은 조합이 7.801로 가장 나은 성능을 보였습니다. 하지만 눈에 띄는 결과물은 아녔기에 변수의 한계를 뚫고자 네 번째 시도를 진행 중입니다.

네번째 시도: extracted_features 활용
-> 모든 변수 사용 시 성능 저하 발생하여 VIF 및 RFECV 실행 중

extracted_features 함수를 통해 변수를 생선 한 결과 1600개 변수가 생성되었습니다. 하지만 결측 값으로 채워진 변수들이 대부분이었으며, 0과 1로 만 이루어진 변수들도 있었기에 이 두 가지 경우를 전처리하여 

121개 변수를 모두 사용하여 랜덤 포레스트의 중요도를 살펴봤습니다. 

중요도의 퍼센트를 보니까 아주 상~당히 낮았습니다. 아무래도 한정된 변수를 121개로 쪼개 놓으니까 설명력이 분산이 된 게 아닌가 싶습니다. 변수 선택을 하기 위해서  VIF, RFECV를 돌리고 있습니다. 결과는 내일 포스팅하겠습니다. 

KNN

k가 3이라면 내 주변에 있는 A라는 집단의 포인트가 2개, B집단의 포인트가 1개가 있다면, A집단이 많으므로 해당 포인트는 A집단으로 분류가 됩니다. 만일 k가 10개 인데 B집단 포인트가 A보다 더 많다면 해당포인트는 B집단으로 분류가 됩니다. 이 내용을 R에서 어떻게 구현할지 실습을 했습니다. 실습 때 사용한 패키지는 caret입니다.

#dependencies = TRUE? : 다른 패키지와 연결이 되도록 하는 명령어(의존성이 있다) 
install.packages('caret', dependencies = TRUE)

##데이터 불러오기
library(caret)
rawdata <- read.csv(file='wine.csv', header=TRUE)
rawdata$Class <- as.factor(rawdata$Class) #Class를 숫자로 인식하지 않도록 factor를 이용
str(rawdata)
View(rawdata)

##데이터분할
analdata <- rawdata
set.seed(2020) #분할시 같은 랜덤이 나오게끔 설정
#sample(x,y): x중에 y만큼 뽑겠다
datatoal <- sort(sample(nrow(analdata),nrow(analdata)*0.7))
train <- rawdata[datatoal,]
test <- rawdata[-datatoal,] #-붙여서 0.7에 뽑힌게 아닌! 데이터를 가져온다

train_x <- train[,1:13]
train_y <- train[,14]

test_x <- test[,1:13]
test_y <- test[,14]

#모형학습
ctrl <- trainControl(method='repeatedcv', number=10,repeats = 5) #number: K-fold의 K(데이터를 10개로 나눈다, 반복횟수 5회
customGrid <- expand.grid(k=1:10) #knn은 1~10까지 보겠다(최 근전 1개 부터 10개까지)
knnFit <- train(Class~., #.은 모든 피쳐를 사용
          data=train,
          method='knn',
          trControl=ctrl, #traincontrol
          preProcess=c("center","scale"), #전처리는 표준화로 실행
          tuneGrid=customGrid,
          metric="Accuracy")
knnFit #출력물의 k은 Knn의 K이다

가장 높은 정확도를 보인 k=5라는 결과가 나왔습니다. 이 모델을 가지고 예측을 진행합니다

#예측하기
pred_test <- predict(knnFit, newdata=test)
confusionMatrix(pred_test, test$Class)

Confusion 매트릭스를 보면 틀린 포인트가 총 3개로 정확도 94%로 계산되었습니다. 

Logitstic

선혀회귀 방식을 분류에 적용한 알고리즘입니다. 간략하게 적어보자면, 선형은 구불거리지 않고 쭉 펼처진 직선 모양을 가집니다. 로지스틱은 직선의 형태가 아니라 시그모이드 형태를 적용합니다. 선형회귀는 만일 집값을 예측할때, A 집값 1억6천만원 과 같은 구체적인 값이 나옵니다. 반면 시그모이드를 취하면 확률이 나옵니다. 보통 0.5 기준으로 0과1로 치환하여 분류를 하게 되기 때문에 분류모형으로 사용될수 있습니다.

#데이터 불러오기
library(caret)
rawdata <- read.csv(file='heart.csv', header = TRUE)
str(rawdata)

#타켓 클래스 범주화
rawdata$target <- as.factor(rawdata$target)
unique(rawdata$target)

#연속형 독립변수의 표준화
rawdata$age <- scale(rawdata$age)
rawdata$trestbps <- scale(rawdata$trestbps)
rawdata$chol <- scale(rawdata$chol)
rawdata$thalach <- scale(rawdata$thalach)
rawdata$oldpeak <- scale(rawdata$oldpeak)
rawdata$slope <- scale(rawdata$slope)

#범주형 독립변수 as.factor : 명복변수를 factor로 만든다
newdata <- rawdata
factorVar <- c('sex','cp','fbs','restecg','exang','ca','thal')
newdata[,factorVar] = lapply(newdata[,factorVar],factor)

#데이터 분리
set.seed(2020)
datatotal <-  sort(sample(nrow(newdata),size=nrow(newdata)*0.7))
train <- newdata[datatotal,]
test <-  newdata[-datatoal,]

train_x <- train[,1:12]
train_y <- train[,13]

test_x <- test[,1:12]
test_y <- test[,13]

#모델설정
ctrl <- trainControl(method='repeatedcv',repeats = 5)
logitFit <- train(target~.,
                  data=train,
                  method="LogitBoost",
                  trControl=ctrl,
                  metric="Accuracy")
logitFit #21번 반복 학습 할때 가장 좋다. 즉 21번

#예측
pred_test <- predict(logitFit,newdata=test)

R

이번 part는 R을 직접 다루는 것이 아니라 머신러닝에 대한 전체적인 개요를 훑은 part였습니다.

이는 다른 강의에서 몇번 중첩된 내용이 대부분이였기 때문에 복습의 개념으로 쭉 봤습니다.

덕분에 잊고 있었던 부분과 평소 알고 싶었던 것들을 간략하게 정리 할수 있었던 시간이였습니다.

특히 likelihood는 작년 처음 수학공부했을때, 한창 혼란스러웠던 시기라서 개념조차 어렵다고만 생각했는데 지금 들으니까 한결 이해하기가 편했습니다. 솔~직히 깊은 내용의 강의가 아니라 머신러닝의 개요 수준이라서 제가 아는 범위였기 때문에 집중력이 많이 떨어지긴 했습니다;;  그래도 꾸역꾸역 들으면서 수강완료를 했습니다 

필기부분은 제가 까먹고 있었거나 하는 내용을 위주로 적었습니다. 저만 볼 생각에 대충 적었는데 보기 불편 하시다면 양해 부탁드립니다 ><

*확률변수-> 숫자로 맵핑 시켜주는 것.
ex)우리집에서 천왕역을 가는 방법
사거리->네네치킨->천황역: 1
사거리->초등학교->천황역: 1
사거리->풍성마트->천황역: 1 
세가지 경우가 있을때 각 경우를 숫자로 맵핑 시켜주는 것을 
이산 확률 변수

확률분포->확률변수값을 확률로 대응시키는 함수를 확률 분포라고 한다.
사거리->네네치킨->천황역: 1, 1/3
사거리->초등학교->천황역: 1, 1/3
사거리->풍성마트->천황역: 1, 1/3 

*MLE : 모수를 추정하는 방법 중 하나이다.
likelihood를 최대화 하는 모수를 추정한다.
likelihood? 이미 주어진 표본적 증거를 토대로 모집단에 관해 통계적 추정이
그럴듯한 정도. 
ex) 뽑은 데이터를 토대로 뮤=5로 놓으면 그럴듯 하겠다


회귀분석part
SST= SSE+SSR
SSR이 많아야 제대로된 회귀식이다. 이를 이용하여 결정계수로 나타낼수있다
R^2 = 1-SSE/SST = SSR/SST

결정계수는 유의하지 않는 변수가 추가 되어도 값이 올라가는 문제점이 있다. 
이를 해결하기 위해서 수정 결정계수가 나타남

다중선형회귀 계수 해석시
다른 독립변수가 고정되었을때의 변화량이다. 
예를들어 y =10+10x1+20x2 에서 x1은 광고비, x2 판매원 수이다. 
이때 광고비의 10은 판매원 수의 값이 고정 되었을때의 10이 나온다는 의미

스케일이 작은 데이터의 오차를 상대적으로 추정하기 위해서 MAPE를 사용

태양열 예측

저번 시간에 문제였던 예측값과 True 값의 벌이짐을 해결했습니다. 여러가지 실험하다가 스케일러를 Robust로 바꾸니까 겹쳐졌습니다. 하지만 여전히 자기상관, 등분산성,정규성을 만족을 못하고 있기 때문에 정상성을 못만들고 있습니다.

R

가설검정 이론 바탕으로한 실습을 진행했습니다. 이번 강의를 통해 다소 헷갈렸던 가설검정을 정리 할수 있었던 좋은 시간이였습니다. 강의 들으면서 필기 했던 부분을 짧게나마 정리하여 간단하게 적어 보겠습니다.

* 대립가설은 보통 양측검정 보다는 단측검정을 사용한다(가설 설정하기 전에 데이터를 대략 파악하여 관계를 설정한다)

* 분할표는 주로 연관성을 볼때 사용한다(예를들어 흡연과 폐암의 연관성) -> 카이제곱 검정

* 대응표본 t검정은 A,B 집단에 속한 대상자가 같다 (예를들어 성형하기 전/후 처럼 대상자는 같고 전/후로 나뉜 경우를 말한다)

* 모집단에 대해서 주의할점: 모집단은 관심이 있는 전체 집단이다. 경기도 20대 남성 평균키일 경우, 모집단은 경기도에 살고 있는 모든 20대 남성들의 키 모음이다.

* t검정은 30개 미만일때 사용하는 것이므로 t검정하기전에 정규성 검정을 하고 등분산 검정을 거친 후 t검정을 적용한다

이때, 정규성 데이터가 아니라면 t검정 대신 비모수 검정을 실시 할수 있다.

* t분포는 정규분포보다 꼬리가 더 두껍다. 그리고 t분포의 n이 커질수록 정규분포에 수렴한다.

*p-value란 귀무가설이 참이라고 했을때, 표본데이터가 수집될 확률을 말한다. 즉, p-value가 낮으면 표본 데이터가 수집될 확률도 낮다. 낮을수록 극단치로 향해 간다. 

*anova는 세 집단 이상일때 사용한다. 아노바의 오차는 집단 간 오차 +집단 내 오차 로 구성된다. 

집단 내 오차는 왜 구하는걸까?

만일 집단 간 오차 > 집단 내 오차 일 경우에는 집단간의 차이가 크다는 얘기이므로 집단 간 평균 차이가 있다는 걸 알수가 있다. 

아래는 가설검정 실습 내용입니다.

rawN3 <- read.csv(file = 'htest01.csv', header = TRUE)
library(dplyr)

groupA <- rawN3[rawN3$group=='A',1:2] 
groupB <- rawN3[rawN3$group=='B',1:2]
mean(groupA[,2])
mean(groupB$height)
#step1: 가설검정 설정
#귀무: 두 집단간의 차이가 없다
#대립: B그룹이 A그룹보다 크다

#step2: 데이터 정규성 검정
#첫번째 방법: 샤피로 검정
shapiro.test(groupA[,2]) #0.05보다 크므로 귀무가설
shapiro.test(groupB[,2])
#qq plot
qqnorm(groupA[,2])
qqline(groupA[,2])

qqnorm(groupB[,2])
qqline(groupB[,2])
#정규성의 직선에 점이 가까울수록 정규성을 따른다

#step3: 분산동질성 검정
#귀무: 두 집단 간 분산은 동일하다
#대립: 분산이 서로 다르다
var.test(groupA[,2],groupB[,2]) #0.05보다 크므로 귀무

#step4: T-test(합동분산 사용)
#alternative: 대립가설 뜻함
#less: A<B(왼쪽집단<오른쪽집단)
t.test(groupA[,2],groupB[,2], alternative = 'less', var.equal = TRUE)

#step5: 0.05보다 크므로 그룹 간 평균키 차이가 없다

#==============================================
#각 집단 샘플 사이즈 = 10(소표본)
rawN10 <-  read.csv(file = 'htest02.csv',header = TRUE)
groupA <- rawN10[rawN10$group=='A',1:2]
groupB <- rawN10[rawN10$group=='B',1:2]
mean(groupA[,2]) #170
mean(groupB[,2]) #181

#step1: 가설설정
#귀무: 평균 키 차이가 없다
#대립: B가 A보다 크다

#step2: 정규성 검정
shapiro.test(groupA[,2]) #정규성따름
shapiro.test(groupB[,2]) #정규성따름

qqnorm(groupA[,2])
qqline(groupA[,2])
qqnorm(groupB[,2])
qqline(groupB[,2])

#step3: 분산 동질성 검정
var.test(groupA[,2],groupB[,2])
#0.02 이므로 대립가설 채택(분산이 다르다)

#step4: T-test 검정
t.test(groupA[,2],groupB[,2], alternative = 'less', var.equal = FALSE)

#step5: 0.019이므로 대립가설 채택(B가A보다 평균키 크다)

#==============================================
#대응표본 t검정(마케팅에 따른 판매액 차이)
raw_d <-  read.csv(file = 'htest02d.csv',header = TRUE)
raw_d
groupAd <- raw_d[,1]
groupBd <- raw_d[,2]
mean(groupAd)
mean(groupBd)

#step1: 가설검정
#귀무: 마케팅을 통한 판매액 변화 없음
#대립: 마케팅을 통한 팬매액이 증가함  전<후

#step2: 데이터 정규성 검정
d= groupAd-groupBd #차이를 가지고 연산
shapiro.test(d) #귀무가설
qqnorm(d)
qqline(d)

#분산동질성 검정이 없는이유
#-> d라는 집단 하나만 있기 때문에

#step3: T-test
t.test(groupAd,groupBd,alternative = 'less',paired=TRUE)

#step4: 0.05보다 작으므로 마케팅을 통해 판매액 증가했다 

#===========================================
#Z검정(데이터 갯수가 30개 이상): 대표본
rawN30 <-  read.csv(file = 'htest03.csv',header = TRUE)
groupA <- rawN30[rawN30$group=='A',1:2]
groupB <- rawN30[rawN30$group=='B',1:2]
mean(groupA[,2])
mean(groupB[,2])

#step1:가설검정
#귀무: 그룹간의 평균 키 차이가 없다
#대립: 그룹B의 평균키가 A 그룹보다 크다

#step2~3: Z-test, 결론
z.test(groupA[,2],groupB[,2]) #대립가설 채택

#=============================================
#여러지단 비교 검정(집단내오차, 집단간오차 필요)
rawN30 <-  read.csv(file = 'htest04.csv',header = TRUE)
groupA <- rawN30[rawN30$group=='A',1:2]
groupB <- rawN30[rawN30$group=='B',1:2]
groupC <- rawN30[rawN30$group=='C',1:2]

#step1: 가설검정
#귀무:세 집단간 평균 차이가 없다
#대립: 세 집단간 평균 차이가 있다(집단이 세개 이상이므로 단측검정할 사용한 방향 설정이 어렵다 따라서 양측검정을 사용)

#step2: 정규성 검정
shapiro.test(groupA[,2]) #귀무
shapiro.test(groupB[,2]) #귀무
shapiro.test(groupC[,2]) #귀무

#step3:분산 동질성 검정
#아노바의 분산 검정은 levene, bartlett test 사용
install.packages('lawstat')
library(lawstat)

levene.test(rawN30$height, rawN30$group)
#세 집단간 분산이 동일하다

bartlett.test(height~group, data=rawN30)

#step3: anova test
rawAnova <- aov(height~group, data=rawN30)
summary(rawAnova)
#p_value가 0.05보다 작으므로 대립가설 채택
#즉, 세 집단간 평균이 다르다
#658.4:그룹 간 오차
#36.2: 그룹 내 오차

#=============================================
#분할표를 이용한 연관성 분석(카이제곱검정)
raw_chisq<-  read.csv(file = 'htest05.csv',header = TRUE)
rawTable <- table(raw_chisq)
rawTable

#step1:가설 설정
#귀무: 흡연여부와 폐암은 관계가 없다
#대립: 관계가 있다

#step2: 카이제곱 검정
#기대도수 >5 인 경우: correct=FALSE
#기대도수<5 인 경우: correct=TRUE
chisq.test(rawTable, correct = FALSE)
#0.05보다 작으므로 대립채택

R

오늘은 R 전처리를 위한 기본 다지기 강의를 들으면서 실습을 진행했습니다 

part3는 기본기 다지기 과정이라서 실습코드는 따로 올리지 않을려고 합니다.

간략하게 학습내용을 적어보자면 산점도,막대그래프,박스플롯,결측치 처리,이상치 정제 그리고 마지막엔 한국복지패널 데이터를 가지고 분석해 보는 실습을 진행했습니다. 

학습내용중에 조금 버벅거리고 낯선 함수가 있습니다. 바로 mutate 함수 입니다. 함수를 통해 변수를 생성하는 것과 직접 $로 변수를 생성하는 코드 과정이 조금 헷갈리는 것같아요 

이 함수를 좀더 주의깊게 봐야 할것 같습니다. 내일은 part4 가설검정을 학습 합니다. 

태양열예측

모든 변수를 넣었을때의 결과 값과 REV로 선별된 변수로 돌린 결과값이 상당히 차이나게 나왔습니다(파라미터는 같게)

게다가 REV에서 선별된 변수로 했을경우에 val 시각화가 이상했습니다. 

True 값과 pred 값이 서로 겹치지 않고 위 아래로 따로 분리가 되었습니다. 패턴은 따라가는 것같은데 

예측값이 True 값과 전혀 달라서 조금도 겹쳐지지 않았습니다. 그러다 보니 성능도 안좋게 나왔구요

거의 점수가 47이 나왔습니다(데이콘의 베이스 코드 점수는 8점대) 데이콘 점수와 크게 차이가 납니다.

시간이 오래 걸려서 train 값을 2020년만 따로 짤라서 하고 있는데도 불구하고 걸리다 보니까 진도가 빨리 안나간다는 점이 안타깝습니다 다음주면 pro 기간 만료라서 더 조급합니다

오늘 새롭게 계획을 세웠습니다. 그 첫걸음은 R! 

작년에 R 강의 들으면서 공부하다가 중간에 중단을 하게 되었습니다. 살짝 늦은 감이 있는 것같지만

처음부터 강의 들으면서 공부하려고 합니다. 

가장 베스트는 이번달 안에 태양열에너지 프로젝트 + R 온라인 완강이 목표입니다.

그래서 틈틈히 R공부하면서 태양프로젝트까지 같이 하고 있습니다. 

오늘 R 배운 내용은 처음부터 하는 거라 가장 기본적인 것들이였습니다. 그래서 실습으로 업로드 하기엔 아닌것 같아서 

이 기록장에 간단하게 열거로 기록하겠습니다.

1. R studio 설치 및 사용법

2. 데이터 분석 기본기 (아래 진도 나간 부분)

 작년에 모두 배웠던 내용이였는지라 이해하기 편했습니다. 

아 그리고 6월달 목표한 R + 프로젝트가 계획대로 끝난다면 바로 computer vision 중급 과정을 배우려고 합니다. 

이미지와 관련된 학문이므로 딥러닝이 반드시 나올텐데, 이때 제가 배우고 있었던 딥러닝수학을 함께 병행하면서 

이해력을 높히고자 합니다. 

요약하자면

6월 : 태양열 에너지 프로젝트 + R 완강&실습

7월 : computer vision 중급 + 딥러닝 수학

8월 : 태블루,SQL,하둡 or ADSP자격증 시험 준비를 계획중입니다.

*태양 프로젝트

오늘은 로그 정규화 하기 전후를 비교 해봤습니다.

두 그래프의 눈에 띄는 차이점은 에너지값 0에 대한 예측값입니다. log를 취해주면 0을 0이라 인식하고 

log를 하지 않으면 마이너스값을 출력합니다. 사실 그동안 0값을 마이너스값으로 예측하는 점 때문에 고민을 많이 했었습니다. 그래서 저 두 결과값을 합쳐봤습니다. 

성능값이 그닥 좋지 않습니다. 두 결과값에 각각 비율을 할당해도 성능은 제자리 걸음이였습니다.

현재 val 값이 가장 좋은 모델은 랜덤입니다. 저는 시계열 모델로 어떻게든 성능을 뽑아 내고 싶은데 쉽지 않습니다.

내일은 log정규화 상태에서 성능을 어떻게 하면 더 끌어 올릴지 연구 해봐야 할것같습니다